Downloads
Download


This work is licensed under a Creative Commons Attribution 4.0 International License.
Review
Microscopic Modelling of Car-Following Behaviour: Developments and Future Directions
Yinglong He 1, * , Quan Zhou 2, * , Chongming Wang 3, Ji Li 2, Bin Shuai 2, Lei Lei 4, and Hongming Xu 2
1 School of Mechanical Engineering Sciences, University of Surrey, Guildford GU2 7XH, UK
2 Department of Mechanical Engineering, University of Birmingham, Birmingham B15 2TT, UK
3 Institutes for Future Transport and Cities, Coventry University, Coventry CV1 5FB, UK
4 College of Information Science and Engineering, Jiaxing University, Jiaxing 314001, China
* Correspondence: yinglong.he@surrey.ac.uk (Y.H.); q.zhou@bham.ac.uk (Q.Z.)
Received: 17 April 2023
Accepted: 21 June 2023
Published: 27 June 2023
Abstract: The study of driving behaviour has become increasingly important in the development of transport and vehicle technologies. Microscopic traffic models simulate individual driver behaviour to understand and predict traffic flow. One of the key components in microscopic simulation is the car-following (CF) model, which describes the behaviour of vehicles in terms of how they follow the vehicle in front of them. Some excellent reviews of CF models are available, however, to the best of the authors’ knowledge, none of them provides a comprehensive analysis that covers and compares different model categories including kinematics-based, dynamics-based, psychological-based, and learning-based. This paper, therefore, provides an overview of the developments and future directions of CF models, encompassing all the previously mentioned categories. It first introduces the fundamental concepts of traffic models, in particular CF models. It then reviews the progress of CF models, which are classified into the above four categories. The advantages and limitations of existing CF models are discussed. The paper further identifies several research directions for future work, including the integration of emerging vehicle technologies, the incorporation of real-world traffic data, and the calibration and validation of model parameters. It concludes by emphasizing the importance of interdisciplinary collaboration and the need for further research to improve the accuracy and practicality of CF models.
Keywords:
car-following model traffic flow vehicle dynamics data-driven1. Introduction
Traffic flow is a complex phenomenon, characterized by the intricate interactions of various elements such as vehicles, drivers, and infrastructure [1]. Moreover, the emergence of automated and electrified vehicles (AEVs) is rapidly revolutionizing the global transportation landscape. In this context, traffic modelling serves as a valuable and efficient tool for comprehensively understanding and assessing these advancements before their implementation on the roads [2]. Through the simulation of vehicle behaviour and interactions, traffic modelling offers a cost-effective means to evaluate and refine such technologies. For instance, virtual environments can be employed to test self-driving cars, allowing engineers to simulate diverse scenarios like unexpected obstacles, adverse weather conditions, and human errors. This facilitates the assessment of autonomous system performance and the identification of areas for improvement prior to real-world trials [3]. Additionally, traffic modelling plays a pivotal role in the development of electric vehicles, enabling researchers to optimize battery performance, charging systems, and analyse the effects of different driving conditions and usage patterns on vehicle range and durability [4,5]. The utilization of traffic models extends beyond technological advancements, as they aid in optimizing infrastructure design, enhancing traffic operations, and informing decision-making regarding traffic management strategies. Moreover, they facilitate the evaluation of potential outcomes resulting from the implementation of novel transportation initiatives, such as intelligent transportation systems, congestion pricing, and sustainable transportation measures. In summary, traffic models are indispensable tools that promote evidence-based decision-making, while concurrently enhancing the efficiency, safety, and sustainability of transportation systems.
Traffic models can be broadly categorized into three types: macroscopic, mesoscopic, and microscopic modelling [6], which vary in the level of detail they provide and the scope of their application. Macroscopic models are used by transport planners to manage large-scale traffic networks, such as motorways, freeways, corridors, urban traffic congestion, and mass transit operations [1]. These models consider the deterministic characteristics of the traffic, such as speed, flow, and density. On the other hand, microscopic simulation models record the behaviour of individual vehicles for each simulation time step based on car-following, lane-changing, and gap-acceptance algorithms [7,8]. They are used to model complex urban street network systems, interchanges, pedestrian movements, traffic signals, multi-modal systems, and proposed mitigations for existing network problems. Mesoscopic models combine both macroscopic and microscopic simulation models and provide less detailed information for individual vehicles compared to micro-simulation [9]. They are typically used for transport planning analysis techniques. In the context of the development of AEVs, micro-simulation is particularly important as it provides a detailed understanding of the impact of each individual AEV on the road network [10]. This is especially useful in the early stages of adoption, where there may be low penetrations of AEVs on the road. By analyzing the behaviour of AEVs in a micro-simulation environment, valuable insights can be gained for their future development and deployment.
One of the key components of a microscopic traffic simulation model is the car-following (CF) model. CF models describe the behaviour of vehicles in terms of how they follow the vehicle in front of them [11,12]. These models are used to simulate the acceleration and deceleration of individual vehicles and to determine their position, speed, and acceleration at any point in time [13]. CF models have proven to be valuable tools in understanding and advancing various aspects of intelligent transportation systems (ITS), traffic management strategies, and vehicle automation technologies. For example, Lee et al. [14] and Jiao et al. [15] have conducted studies showcasing the utilization of CF models to analyse traffic flow dynamics and improve road safety. The work of Yu et al. [1] illustrates how CF models have been applied to assess the interactions between human-driven vehicles and connected and automated vehicles (CAVs). These examples highlight the practical applications of CF models in addressing key challenges in transportation and automotive engineering. From different perspectives, CF models can be categorized into four main types: Kinematics-based, dynamics-based, psychological-based, and learning-based.
Kinematics-based models are the simplest type of CF models, as they assume that drivers adjust their speed based solely on the distance and relative speed between their vehicle and the lead vehicle [16]. These models are based on the assumption that drivers follow a constant time headway, which is the time it takes for a driver to reach the same position as the lead vehicle, given their relative speeds. One of the most well-known kinematics-based models is the Intelligent Driver Model (IDM) [17], which assumes that drivers aim to maintain a constant safe distance from the lead vehicle and that they adjust their speed based on their perceived distance and speed difference.
Dynamics-based CF models take into account the physical properties of the vehicle, such as its mass, engine power, and braking capabilities, as well as the road and weather conditions [4]. These models aim to capture the dynamic behaviour of the vehicle, such as its acceleration and deceleration, and the forces acting on it, such as aerodynamic drag and rolling resistance. It is worth noting that both types of CF models should be able to strike a balance between simplicity and accuracy and therefore feasible for large-scale traffic simulation [18].
Psychological-based CF models seek to capture the cognitive processes and decision-making strategies of human drivers and have been developed based on principles of cognitive psychology and driver behaviour theory [19]. These models assume that drivers are influenced by factors such as their perception of the traffic environment, their expectations of the behaviour of other drivers, and their level of attention and motivation [20].
Learning-based CF models are an emerging class of traffic simulation models that rely on large amounts of observed driving data to learn patterns and relationships between variables that influence driving behaviour [21]. These models are increasingly being used in traffic simulation due to their ability to capture the complex interactions between drivers and their environment and their potential to provide more accurate and reliable traffic flow predictions [22]. Unlike other types of models, learning-based CF models do not rely on assumptions about driver behaviour or decision-making processes. Instead, they use machine learning (ML) techniques such as neural networks (NNs) and decision trees to identify patterns in driving data such as speed, acceleration, and vehicle spacing [23]. In recent years, there has been a significant increase in the development and application of learning-based CF models in traffic simulation. This is due, in part, to the availability of large-scale driving datasets and advances in ML algorithms and computing power [24].
Although numerous studies have investigated CF modelling [1,4,19,24], our research contributes to the field by focusing on innovative approaches that leverage emerging technologies and advanced modelling techniques. By exploring these novel perspectives, we aim to advance the current understanding of CF behaviour and pave the way for smarter and more efficient transportation systems. In this paper, we provide a comprehensive review of the state-of-the-art in CF modelling. Our analysis encompasses various modelling paradigms, including kinematics-based, dynamics-based, psychological-based, and learning-based models. By examining the strengths and limitations of each approach, we identify innovative points that can drive further advancements in CF modelling and contribute to the development of intelligent transportation systems.
2. Kinematics-Based Car-Following (CF) Models
Kinematics-based (or behavioural) CF models describe the movement of the following vehicle as a function of its kinematic relationship to the preceding vehicle and, in the last seven decades, have been studied intensively by model simulation, experimental campaign, and traffic observation [25].
In Table 1, typical kinematics-based CF models are listed chronologically with the deterministic acceleration or speed equation and the associated parameters given in the last two columns [26]. In the early 1950s, Reuschel [27] and Pipes [28] did pioneering work on the development of behavioural CF models. Their model formulations only consider either the inter-vehicle spacing (sn) or the relative velocity (Δvn, between the preceding and ego vehicles), and therefore, have significant limitations in describing the vehicle behaviour [29]. The Gazis–Herman–Rothery (GHR) model, proposed by Gazis et al. in 1961 [30], defines a nonlinear acceleration equation that considers reaction time (τ) [10]. However, it is built upon strong assumptions, leading to critical drawbacks that are frequently reported by researchers, for example, the model overestimates the vehicle’s ability to perceive small changes in the relative speed (Δvn) and the headway (Δxn) [31,32]. Newell’s model assumes that the following vehicle’s response directly depends on the headway (Δxn) [33], which, however, might result in unrealistic acceleration behaviour [34].
Table 1. Typical kinematics-based car-following (CF) models.

* H(·) is Heaviside function.
Source: Adapted from Chen et al. [26,9], Reuschel [27], and Gipps [35] Note: Subscripts n and n-1 indicate the ego and preceding vehicles, respectively; Δxn (t) = xn -1(t) - xn (t) is the headway (m); Δvn (t) = vn -1(t) - vn (t) is the relative speed (m/s); sn (t) = xn -1(t) - xn (t)-ln -1 is the spacing (or gap, m); Vn is the free-flow (or desired) speed; GHR = Gazis-Herman-Rothery model; OV = optimal velocity model; GFM = generalized force model; IDM = intelligent driver model; FVDM = full velocity difference model.
As a major milestone towards the development of safety distance (or collision avoidance) CF models [34], Gipps model [36] developed in 1981 has been extensively studied [11]. It describes the vehicle speed in a way assuming that the driver leaves enough safe distance in front and thus can safely stop the vehicle in case the preceding vehicle commences an emergency brake [36]. Gipps model consists of two driving regimes, i.e., free-flow and congested, and chooses the more restrictive one from the resulting speeds of these two regimes [37].
The optimal velocity (OV) model, proposed by Bando et al. [38], assumes that the vehicle attempts to follow an optimal (or safe) speed (Vopt) that depends on the headway (Δxn). This model has received considerable attention because of its ability to accurately describe many traffic flow characteristics in the real world, e.g., traffic instability, traffic congestion evolution, and the formation of stop-and-go waves. However, a comparison between the simulated and observed vehicle trajectories indicates that the OV model exhibits significantly high acceleration and unrealistic deceleration [39]. To overcome this limitation, Helbing et al. adopted the basic concept of the OV model, utilized negative velocity difference, and developed the generalized force model (GFM), which demonstrates a good agreement with empirical trajectory data [40], but is poor in predicting the delay time of vehicle movement [39]. Consequently, Jiang et al. [41] modified GFM in 2001 by including the negative and positive velocity differences and then proposed the full velocity difference model (FVDM) [39].
The intelligent driver model (IDM), proposed by Treiber et al. [17] in 2000, is a breakthrough in the development of desired measure CF models, which usually assume that vehicles aim to simultaneously reach both the desired (or free-flow) speed (Vn) and the desired spacing (sn ,des). Its acceleration equation can ensure a smooth transition between the free-flow and congested driving regime [34]. Nevertheless, IDM does not provide a lower bound for the acceleration, and therefore, may lead to unrealistic large deceleration when the inter-vehicle spacing (sn) drops significantly (e.g., in cut-in manoeuvres) [45].
3. Dynamics-Based CF Models
Dynamics-based CF models take into account features, e.g., force, torque, and power, underlying the vehicle movement [4]. As summarized in Table 2, it has been a growing field across several disciplines in recent years. Relevant publications remain few, almost all of which focus on conventional ICEVs powered by a gasoline or diesel ICE with a multi-ratio transmission. The pioneering work of Searle et al. [46] is crucial to our wider understanding of this area. In their model, however, the full load (FL) engine power ( ) is assumed to be constant and equal to the peak engine power (
) is assumed to be constant and equal to the peak engine power (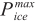 ) across the entire engine speed range. Also, the dynamics of the internal driveline (e.g., transmission and engine accessories) and external resistances (i.e., aerodynamic, rolling, and grade) are not considered; instead, their effects on the power losses are all incorporated into a constant, i.e., acceleration efficiency (ηa). Moreover, driving behaviour, that is, how the driver utilizes the vehicle’s full load capabilities, is not indicated, thus, the model’s output is the maximum acceleration characteristics. In the subsequent study by Rakha et al. [47], the enhanced model accounts for detailed dynamics of the driveline and the resistances. Although the full load engine power (
) across the entire engine speed range. Also, the dynamics of the internal driveline (e.g., transmission and engine accessories) and external resistances (i.e., aerodynamic, rolling, and grade) are not considered; instead, their effects on the power losses are all incorporated into a constant, i.e., acceleration efficiency (ηa). Moreover, driving behaviour, that is, how the driver utilizes the vehicle’s full load capabilities, is not indicated, thus, the model’s output is the maximum acceleration characteristics. In the subsequent study by Rakha et al. [47], the enhanced model accounts for detailed dynamics of the driveline and the resistances. Although the full load engine power ( ) is still constant, the tractive force is upper bounded by the maximum force that can be sustained between the vehicle tires and the road surface. Rakha et al. [48] then developed a variable power dynamics model in 2002 by introducing a power adjustment factor (β), which dealt with the full load power reduction caused by the effect of successive gear shifting at low speeds. The factor β is a ramp function (with a positive intercept) of vehicle speed (vn), when vn ≤ vp (vp is the speed at which maximum power occurs).
) is still constant, the tractive force is upper bounded by the maximum force that can be sustained between the vehicle tires and the road surface. Rakha et al. [48] then developed a variable power dynamics model in 2002 by introducing a power adjustment factor (β), which dealt with the full load power reduction caused by the effect of successive gear shifting at low speeds. The factor β is a ramp function (with a positive intercept) of vehicle speed (vn), when vn ≤ vp (vp is the speed at which maximum power occurs).
Table 2. Development of dynamics-based car-following (CF) models.

* The ICE full load power (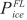 ) across the entire operating speed range can be calculated in three ways: 1)
) across the entire operating speed range can be calculated in three ways: 1)  , which is a constant and equal to the peak power that the ICE can produce; 2)
, which is a constant and equal to the peak power that the ICE can produce; 2) 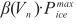 , which is a percentage of the ICE peak power; or 3)
, which is a percentage of the ICE peak power; or 3) 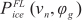 , which is a function of the vehicle speed vn and the engaged gear ratio φg .
, which is a function of the vehicle speed vn and the engaged gear ratio φg .
** The gear shifting points within the vehicle speed range are defined by wgb for each driver.
*** The driver’s typical driving behaviour can be represented as a percentage of the vehicle’s full load capabilities in two ways: 1) to multiply the full load ICE power curve by a power reduction (or throttle opening) factor, tdb ; or 2) to multiply the vehicle’s acceleration potential curve by an acceleration reduction factor, wdb . Both of the above factors can be a constant or a function (the symbol with arguments in parentheses) for each driver.
**** Collision avoidance and traffic stability, both of which belong to the interaction term (instead of the free-flow term) of the CF model, can be either formulated as speed limit functions (i.e., 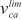 and
and 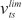 , respectively) or directly incorporated into the driving behaviour function wdb.
, respectively) or directly incorporated into the driving behaviour function wdb.
Source: Adapted from He et al. [4].
Note: β is the full load power adjustment factor for the ICE; vn and vn -1 are speeds of the ego (n) and preceding (n-1) vehicles, respectively; Vn is the desired or free-flow speed; sn is the inter-vehicle spacing (or gap); GS and DS are calibratable parameters capturing gearshift style and acceleration style, respectively; ICE = internal combustion engine; RPA = Rakha-Pasumarthy- Adjerid model; FR = Fadhloun-Rakha model; MFC = microsimulation free-flow acceleration model.
Rakha et al. [49] are the first of many who have attempted to capture typical driving behaviour and vehicle dynamics at the same time. The typical acceleration output is achieved by introducing an acceleration reduction factor (wdb), which denotes the ratio of the driver’s actual acceleration to the vehicle’s theoretical capability. On the other hand, the model proposed in 2009 by Rakha et al. [50] adopts a power reduction factor (tdb) aiming to represent the percentage of the throttle opening, and therefore, the power delivered from the engine can be assumed to be equal to a constant percentage of the full load engine power. Additionally, to capture the interaction of vehicles in the traffic flow, the model considers two speed constraints:  to avoid any collisions with the preceding vehicle and
to avoid any collisions with the preceding vehicle and 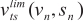 to maintain cruising in the steady-state traffic stream. Rakha et al. [51] developed the first model that explicitly captures the dynamics of engine power and gearshift. This research is critical, given that the full load engine power (
to maintain cruising in the steady-state traffic stream. Rakha et al. [51] developed the first model that explicitly captures the dynamics of engine power and gearshift. This research is critical, given that the full load engine power (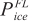 ) during driving cannot be assumed to be constant over the entire vehicle speed range nor to be adjusted by a ramp function (β) at the low-speed region. In fact, it is well known that the engine power at full load conditions varies as a function of the current vehicle speed (vn) and the engaged gear ratio (φg). Moreover, the gearshift behaviour (wgb) in this model is designed as per a fixed engine speed threshold.
) during driving cannot be assumed to be constant over the entire vehicle speed range nor to be adjusted by a ramp function (β) at the low-speed region. In fact, it is well known that the engine power at full load conditions varies as a function of the current vehicle speed (vn) and the engaged gear ratio (φg). Moreover, the gearshift behaviour (wgb) in this model is designed as per a fixed engine speed threshold.
The above three typical acceleration models reported by Rakha et al., however, reproduce the driving behaviour (wdb or tdb) and the gearshift behaviour (wdb) using constant factors, thus they provide limited information in relation to each driver’s unique pattern of driving. Recognizing this deficiency, an enhancement proposed in 2015 by Fadhloun et al. [52] made the model representative of different driving patterns. The basic idea behind their research is to employ a variable throttle opening (tdb) as a function of the vehicle speed (vn) and the driver’s desired speed (Vn). In 2019, Fadhloun et al. [53] further improved the model by incorporating the two constraints regarding vehicle interactions (i.e., collision avoidance and steady-state traffic stream) into the driving behaviour function wdb (vn ,vn -1,Vn ,sn ), which serves as an acceleration reduction factor. Makridis et al. [18] demonstrated the first study to account for different drivers’ driving behaviour and gearshift behaviour simultaneously, by introducing two calibratable parameters, i.e., driving style (DS) and gearshift style (GS).
4. Psychological-Based CF Models
Due to differences in individual drivers and their driving styles and risk-taking abilities, factors such as age and gender can significantly impact the perception of risky driving situations. Additionally, specific driving needs can contribute to aggressive driving, which can increase the likelihood of driving errors [54]. Therefore, a more comprehensive representation of the cognitive processes involved in CF is necessary to accurately describe driver responses and their consequences in adverse driving scenarios. Furthermore, CF models that can replicate a driver’s mistakes and generate crash or near-crash scenarios can serve as valuable tools for evaluating safety technologies and policies [34]. Table 3 provides different psychological-based CF models, which are explained in detail below.
Table 3. Categories of psychological-based car-following (CF) models.
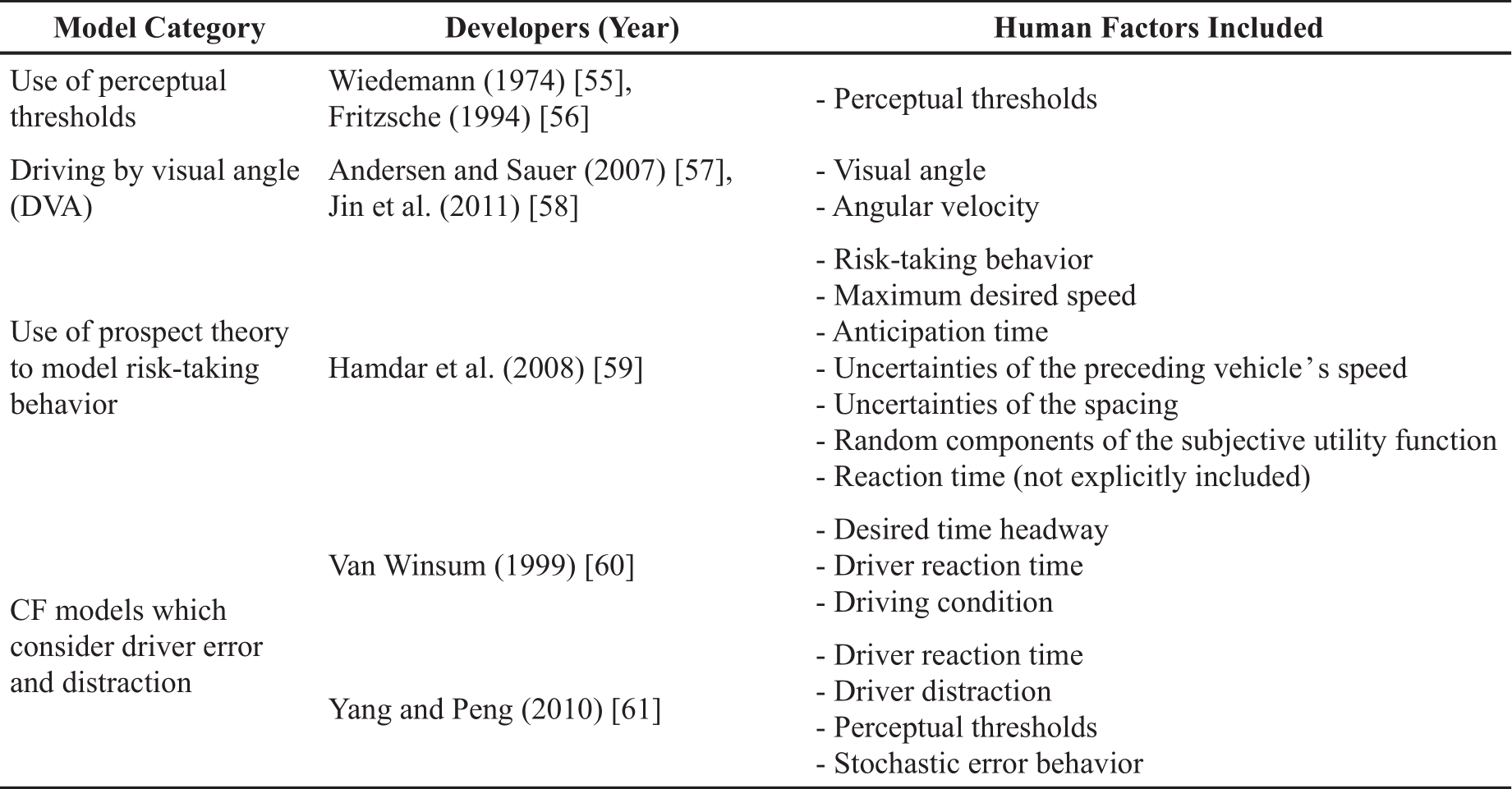
Source: Adapted from Saifuzzaman and Zheng [19,34].
4.1. Use of Perceptual Thresholds
CF models usually make unrealistic assumptions that drivers can accurately perceive and react to even minor changes in their driving environment, such as slight variations in speed difference or spacing. To address this issue, Wiedemann [55] introduced the concept of a “perceptual threshold”, which refers to the minimum stimulus value that a driver can detect and react to. CF models based on this concept are commonly referred to as “psycho-physical” models. The perceptual threshold is determined based on the speed difference and spacing between the leading and following vehicles and varies depending on whether the driver is accelerating or decelerating.
A modified version of the Wiedemann model has been utilized in the VISSIM commercial microsimulation software [62], which has been subject to several calibration attempts documented in the literature. For example, Park and Qi [63] employed Genetic Algorithm to estimate model parameters, while Gomes et al. [64] manually calibrated four of the ten driver behaviour parameters and left the remaining ones as default. Fritzsche [56] proposed a similar CF model, which divides the operating space into five regions: Danger, Closing in, Following I, Following II, and Free Driving. According to the model, a following vehicle will only decrease its speed when it enters either the ’Danger’ or ’Closing in’ regions.
4.2. Driving by Visual Angle (DVA)
According to Michaels [65], a driver’s perception of the driving situation is influenced by the visual size of the preceding vehicle. It has been found that humans can accurately estimate the time to collision (TTC) based on visual angles subtended by the preceding vehicle (that is, visual angle divided by rate of change of visual angle) [66]. The visual angle model, based on Michaels’ assumption [65], suggests that as drivers approach a vehicle in front, they perceive the situation from the changes in the apparent size of the vehicle. Specifically, the relative speed is perceived through the changes in the visual angle subtended by the preceding vehicle. For example, Andersen and Sauer [57] modified Helly’s model [67] by using visual angle as the stimuli. Similarly, Jin et al. [58] modified the full velocity difference model (FVDM) [41] using visual angle.
4.3. Use of Prospect Theory to Model Risk-Taking Behaviour
When driving in risky situations, the cognitive process involves perceiving, judging, and executing a decision-making strategy, such as braking or changing lanes. The expected utility theory, proposed by Von Neumann and Morgenstern in 1949 [68], serves as the basis for modern decision-making theories. However, inconsistencies between the actual decisions made and those predicted by the utility theory have led to the development of more realistic models that accurately describe decision processes. Prospect theory, introduced by Kahneman and Tversky in 1979 [69], is a well-established descriptive model that captures human decision-making in situations involving the possibility of risky outcomes. Moreover, in 2008 and 2015, Hamdar et al. developed a driver behaviour model based on prospect theory [59,70]. Specifically, their model treats driving as a sequential risk-taking task and employs prospect theory to weigh a driver’s alternatives. The subjective probability of being involved in a rear-end collision with the preceding vehicle is the primary variable of interest in their model, which depends on acceleration, spacing, and speed difference.
4.4. Considering Driver Error and Distraction
Driving errors are responsible for most crashes, [71], which can be classified into five groups: action errors, cognitive and decision-making errors, observation errors, information retrieval errors, and violations [54,72]. Any of these errors can affect CF behaviour, and therefore, how and to what extent it is affected has been explored in the literature. For example, Van Winsum [60] extended Helly’s desired spacing model [67] to account for human behaviour by considering the desired time headway, which may differ significantly between drivers depending on various factors such as driving conditions and cognitive demand. Yang and Peng [61] proposed an error-able CF model, which is intended for evaluating active safety technologies (AST), and it is based on a stochastic model with an error mechanism derived from the Road-Departure Crash-Warning System Field Operational Test (RDCW). Using this model, the desired acceleration of the driver can be calculated as a function of several factors, including following distance, speed difference, and time headway. The model also accounts for uncertainties in calculating the final acceleration, recognizing that drivers may not perceive accurately and have more room to deviate when the following distance is large.
5. Learning-Based CF Models
Recently, there has been a growing interest in using artificial intelligence (AI) algorithms and machine learning (ML) techniques to model car-following (CF) behaviour, facilitated by the availability of big data from various sensors, such as GPS data, traffic cameras, and sensors [73]. These models have the advantage of handling large amounts of data and not requiring explicit assumptions about the underlying traffic dynamics. As depicted in Table 4, learning-based CF models can be classified into two main groups: data-driven and physics-informed.
Table 4. A summary of learning-based car-following (CF) models.
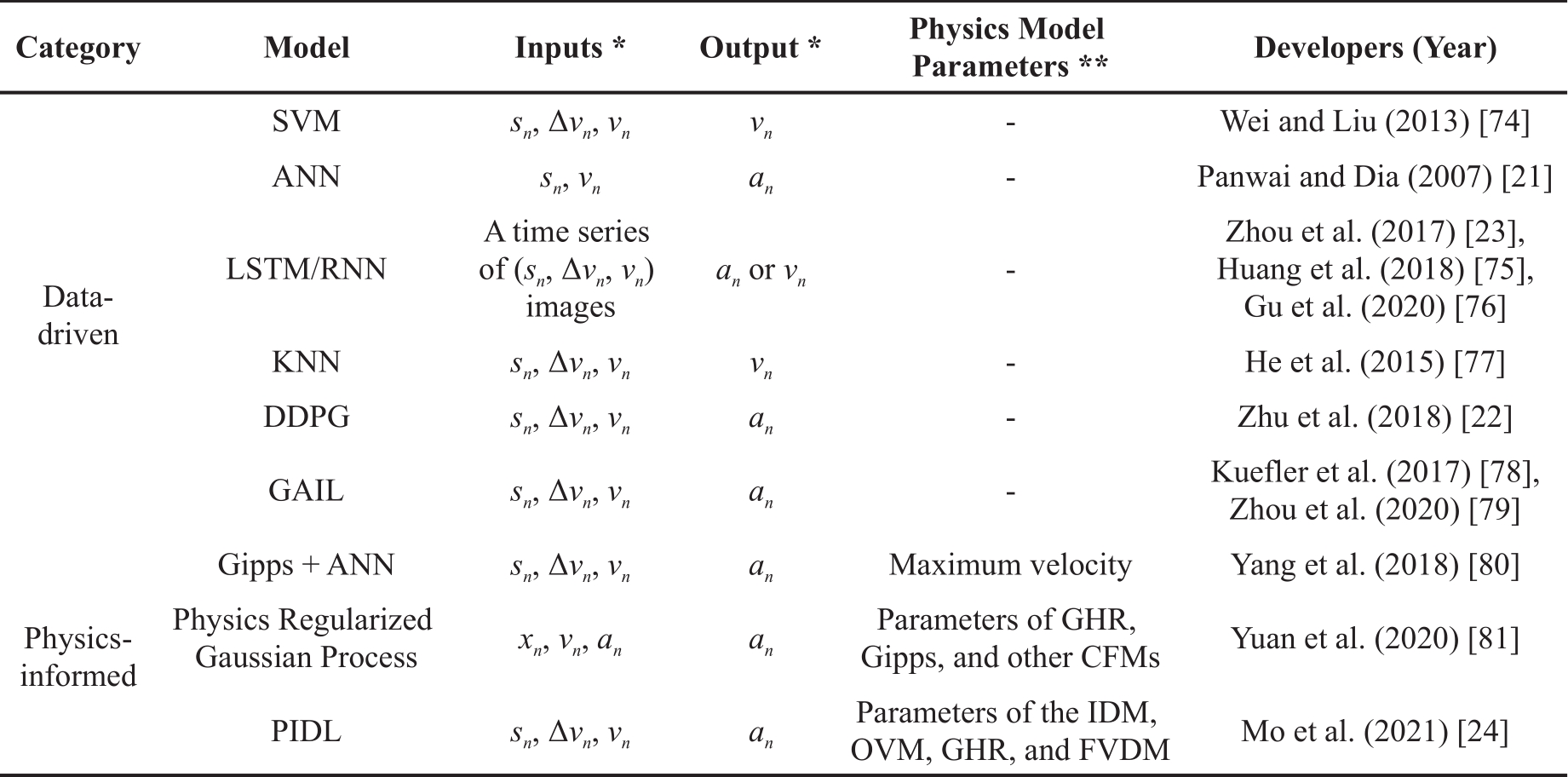
* xn , sn , vn , an are the position (m), spacing (m), velocity (m/s), and acceleration (m/s2) of the ego vehicle, respectively. Δvn is the velocity difference between the ego vehicle and its leader.
** Only parameters related to a physical meaning are listed. Parameters like constant coefficients and sensitivity parameters are not listed.
Source: Adapted from Mo et al. [24].
5.1. Data-Driven Models
Data-driven CF models utilize deep neural networks (DNN), reinforcement learning (RL), imitation learning (IL), and other machine learning techniques to mimic human intelligence. These models do not have a predetermined mathematical form and rely solely on observations for training.
There is a rising trend in employing (deep) neural networks (NN) in data-driven models. The pioneering study by Panwai and Dia [21] utilized an artificial neural network (ANN) model to simulate car-following behaviour, and the results indicated that the ANN model outperformed kinematics-based models like Gipps regarding overall prediction accuracy and robustness. Data-driven models can also better capture asymmetric car-following behaviours, which can not be well solved by traditional CF models. For example, recurrent neural networks (RNN) and Long Short-Term Memory (LSTM) models [23,75,76,82] are other types of neural networks that can leverage historical data to learn asymmetric behaviours resulting from different driving patterns in free-flow and stop-and-go regimes. He et al., [77] proposed a nonparametric CF model based on k-nearest neighbour (KNN), which can replicate periodic traffic oscillations, from the precursor stage to the decay stage, and does so without any assumptions. Zhu et al. [22] developed a CF model based on deep reinforcement learning, which is optimized using deep deterministic policy gradient (DDPG) algorithm. The model is capable of replicating human-like car-following behaviour more accurately than both traditional and recent data-driven CF models. Studies have recently highlighted the benefits of employing reinforcement learning techniques in CF models. Nonetheless, there is still an issue with determining the reward function manually. To address this problem, previous studies introduce novel CF models that utilize generative adversarial imitation learning, which can learn the driver’s strategy from demonstrations without the need to specify the reward [78,79].
5.2. Hybrid Models
Both traditional (e.g., Kinematics-, dynamics-, and psychological-based) models and data-driven models have their advantages and disadvantages. Traditional models may not be generalizable as they rely on predefined motion heuristics that make strong assumptions about driving behaviours with a limited set of parameters. This approach may not capture human strategic planning behaviours and may not generalize well to diverse driving scenarios in a highly interactive environment. In contrast, data-driven models are data-hungry, requiring a large amount of driving data to calibrate. They also lack interpretability, making it difficult to gain insights into how driving behaviour evolves as the traffic environment changes. Furthermore, data-driven models are more vulnerable to data noise and unseen data compared to traditional models. Driving data, usually measured by GPS sensors, is sparse due to high installation and data acquisition costs. Thus, a paradigm that is both data-efficient and highly accurate is preferred.
Several studies have explored to develop physics-informed CF models that leverage the advantages of both traditional (data-efficient and interpretable) and data-driven (generalizable) models [24]. Yang et al. [80] integrated the Gipps model with deep learning (DL)-based models such as back-propagation NNs and random forest to develop a combined model that selects optimal weights for collision avoidance of predicted trajectories. This model can reconstruct trajectories that balance authenticity and safety, and the Gipps model and DL-based models are trained independently. In addition to the NN-based model, Yuan et al. [81] introduced a physics regularized Gaussian process model by incorporating traditional CF models into a Gaussian Process model to predict driver accelerations. In this study, we propose two methods to hybridize physics into NNs by encoding the physics into the NN structure to regulate the NN training. Mo et al. [24] developed physics-informed deep learning CF model (PIDL-CF) architectures encoded with 4 popular kinematics-based models—the IDM, the optimal velocity (OV) model, the Gazis-Herman-Rothery (GHR) model, and the full velocity difference model (FVDM). The results demonstrate the superior performance of neural networks informed by physics over those without.
6. Research Outlook
Despite considerable advancements made in the field of driving behaviour modelling, especially in car-following models, there are still numerous challenges and possibilities for further exploration in this area.
6.1. Model Development
Despite the many car-following models that have been developed, there is still a need for models that can capture the complex interactions between drivers and their environment. Future research should focus on developing models that can better account for driver decision-making processes, such as risk perception and anticipation. Additionally, there is a need for models that can capture the effects of emerging technologies, such as electric and autonomous vehicles.
As the interactions between different types of vehicles, such as human-driven vehicles (HDVs) and automated vehicles (AVs) with varying automation levels, become more complex, coupled with high dimensionality and uncertainty, and given that most major AV driving systems rely heavily on AI algorithms, the traffic flow community is increasingly seeking to improve existing traffic flow models by integrating AI techniques, or develop entirely new traffic flow models based solely on AI. This is particularly important as real-world AV data become more readily available, and AI techniques become increasingly adept at handling large numbers of parameters.
Moreover, it is important to carefully consider the interaction between transportation infrastructure management and mixed traffic flow, as both HDVs and AVs are expected to coexist on roads for a significant period of time. Further discussions are necessary to fully comprehend the complexity of this critical issue.
6.2. Model Calibration and Validation
Calibrating and validating car-following models is a challenging task, particularly when using real-world driving data. Future research should focus on developing new calibration and validation techniques that can account for the uncertainties and heterogeneity of driving data. Additionally, it is crucial to evaluate and validate models in specific traffic scenarios to ensure their accuracy and applicability. Different scenarios may require different model parameters or adaptations to accurately represent real-world behaviour. Standardized protocols for calibration and validation should be established to ensure the consistency and comparability of model outputs. Furthermore, there is a need for comprehensive performance assessments and comparisons to evaluate model performance under various traffic conditions.
6.3. Data Availability
The availability of large-scale driving datasets has significantly increased in recent years, and this trend is likely to continue in the future. However, there are still challenges in collecting and processing high-quality driving data, particularly in real-world traffic conditions. Future research should focus on developing new data collection techniques that can capture a wide range of driving scenarios, including connected and autonomous vehicles. Additionally, there is a need for standardized data collection protocols to ensure the consistency and comparability of driving data.
Overall, the future of research on driving behaviour modelling is promising. With the continued growth of driving data and the development of new modelling techniques, we can expect to see significant improvements in our understanding of driving behaviour and our ability to predict traffic flow in the years to come.
7. Conclusions
In conclusion, this study has provided a comprehensive overview of the current state-of-the-art in car-following (CF) modelling, with a specific focus on kinematics-based, dynamics-based, psychological-based, and learning-based CF models. We aimed to enhance the understanding of stakeholders in the transportation and automotive research communities regarding recent advances in CF modelling and to identify avenues for future research in this critical field.
The present work has shed light on the innovative aspects of CF modelling, showcasing the potential of emerging technologies and advanced modelling techniques to improve our understanding of traffic flow dynamics. By exploring novel perspectives, such as the application of artificial intelligence (AI) algorithms, machine learning (ML) techniques, and the integration of connected and autonomous vehicles, we have paved the way for significant advancements in CF modelling. This review has highlighted the promising results achieved by learning-based CF models, such as deep neural networks (DNN), reinforcement learning (RL), and imitation learning (IL). These innovative approaches demonstrate the ability to capture complex car-following behaviours by leveraging AI and ML techniques, thus surpassing traditional models’ limitations.
Furthermore, we have underscored the need for standardized protocols for model calibration and validation, as well as the collection and processing of high-quality driving data. The integration of innovative data collection techniques, coupled with the analysis of large-scale driving datasets, holds tremendous potential for enhancing the accuracy and applicability of CF models.
By emphasizing these innovative points, this study contributes to the ongoing research efforts in the field of CF modelling and sets the stage for further exploration. We believe that these findings provide valuable insights for researchers and practitioners interested in developing intelligent transportation systems that can optimise traffic flow and ensure safer and more efficient mobility.
Funding: This research received no external funding.
Data Availability: Not applicable.
Acknowledgments: The authors are grateful to Biagio Ciuffo, Georgios Fontaras, and Konstantinos Mattas from the Joint Research Centre (JRC) of the European Commission, Michail Makridis from ETH Zurich, as well as Vincenzo Punzo and Marcello Montanino from the University of Naples Federico II, for their valuable advice and support. Additionally, the authors extend their appreciation to the anonymous reviewers for their invaluable comments, which greatly enhanced the manuscript's quality.
Conflicts of Interest: The authors declare no conflict of interest.
References
- Yu, H. ; Jiang, R. ; He, Z. ; et al . Automated vehicleinvolved traffic flow studies: A survey of assumptions, models, speculations, and perspectives . Transportation Research Part C: Emerging Technologies 2021 , 127 , 103101 . DOI: https://doi.org/10.1016/j.trc.2021.103101
- He, Y. Developing and evaluating the driving and powertrain systems of automated and electrified vehicles (AEVs) for sustainable transport . thesis, Ph.D. ,University of Birmingham,Birmingham,UK , 2021 .
- He, Y. ; Zhou, Q. ; Makridis, M. ; et al . Multiobjective co-optimization of cooperative adaptive cruise control and energy management strategy for PHEVs . IEEE Transactions on Transportation Electrification 2020 , 6 ( 1 ), 346 – 355 . DOI: https://doi.org/10.1109/TTE.2020.2974588
- He, Y. ; Makridis, M. ; Mattas, K. ; et al . Introducing electrified vehicle dynamics in traffic simulation . Transportation Research Record 2020 , 2674 ( 9 ), 776 – 791 . DOI: https://doi.org/10.1177/0361198120931842
- Commission, European ,Joint Research Centre . The Future of Road Transport – Implications of Automated, Connected, Low-Carbon and Shared Mobility , Publications Office , 2019 . Available Online: https://data.europa.eu/doi/10.2760/668964 (Accessed on 12 June 2023) .
- Ni, D. Multiscale modeling of traffic flow . Mathematica Aeterna 2011 , 1 ( 1 ), 27 – 54 .
- He, Y. ; Mattas, K. ; Dona, R. ; et al . Introducing the effects of road geometry into microscopic traffic models for automated vehicles . IEEE Transactions on Intelligent Transportation Systems 2021 , 23 ( 8 ), 13604 – 13613 . DOI: https://doi.org/10.1109/TITS.2021.3126049
- Punzo, V. ; Montanino, M. ; Ciuffo, B. Do we really need to calibrate all the parameters? Variance-based sensitivity analysis to simplify microscopic traffic flow models . IEEE Transactions on Intelligent Transportation Systems 2014 , 16 ( 1 ), 184 – 193 . DOI: https://doi.org/10.1109/TITS.2014.2331453
- Chen, X. ; Li, L. ; Shi, Q. Stochastic evolutions of dynamic traffic flow . In Modeling and Applications . Springer : New York, NY, USA , 2015 . DOI: https://doi.org/10.1007/978-3-662-44572-3
- Elefteriadou, L. An Introduction to Traffic Flow Theory, Vol . 84 ; Springer: New York, NY, USA, 2014 . DOI: https://doi.org/10.1007/978-1-4614-8435-6
- Ciuffo, B. ; Punzo, V. ; Montanino, M. Thirty years of Gipps’ car-following model: Applications, developments, and new features . Transportation Research Record 2012 , 2315 ( 1 ), 89 – 99 . DOI: https://doi.org/10.3141/2315-10
- Punzo, V. ; Zheng, Z. ; Montanino, M. About calibration of car-following dynamics of automated and human-driven vehicles: Methodology, guidelines and codes . Transportation Research Part C: Emerging Technologies 2021 , 128 , 103165 . DOI: https://doi.org/10.1016/j.trc.2021.103165
- Donà, R. ; Mattas, K. ; He, Y. ; et al . Multianticipation for string stable Adaptive Cruise Control and increased motorway capacity without vehicle-to-vehicle communication . Transportation Research Part C: Emerging Technologies 2022 , 140 , 103687 . DOI: https://doi.org/10.1016/j.trc.2022.103687
- Lee, S. ; Ngoduy, D. ; Keyvan-Ekbatani, M. Integrated deep learning and stochastic car-following model for traffic dynamics on multi-lane freeways . Transportation Research Part C: Emerging Technologies 2019 , 106 , 360 - 377 . DOI: https://doi.org/10.1016/j.trc.2019.07.023
- Jiao, S. ; Zhang, S. ; Zhou, B. ; et al . Dynamic performance and safety analysis of car-following models considering collision sensitivity . Physica A: Statistical Mechanics and Its Applications 2021 , 564 , 125504 . DOI: https://doi.org/10.1016/j.physa.2020.125504
- He, Y. ; Montanino, M. ; Mattas, K. ; et al . Physics-augmented models to simulate commercial adaptive cruise control (ACC) systems . Transportation Research Part C: Emerging Technologies 2022 , 139 , 103692 . DOI: https://doi.org/10.1016/j.trc.2022.103692
- Treiber, M. ; Hennecke, A. ; Helbing, D. Congested traffic states in empirical observations and microscopic simulations . Physical Review E 2000 , 62 ( 2 ), 1805 . DOI: https://doi.org/10.1103/PhysRevE.62.1805
- Makridis, M. ; Fontaras, G. ; Ciuffo, B. ; et al . MFC free-flow model: Introducing vehicle dynamics in microsimulation . Transportation Research Record 2019 , 2673 ( 4 ), 762 – 777 . DOI: https://doi.org/10.1177/0361198119838515
- Saifuzzaman, M. ; Zheng, , Z. Incorporating human-factors in car-following models: a review of recent developments and research needs . Transportation Research Part C: Emerging Technologies 2014 , 48 , 379 – 403 . DOI: https://doi.org/10.1016/j.trc.2014.09.008
- Treiber, M. ; Kesting, A. ; Helbing, D. Delays, inaccuracies and anticipation in microscopic traffic models . Physica A: Statistical Mechanics and Its Applications 2006 , 360 ( 1 ), 71 – 88 . DOI: https://doi.org/10.1016/j.physa.2005.05.001
- Panwai, S. ; Dia, H. Neural agent car-following models . IEEE Transactions on Intelligent Transportation Systems 2007 , 8 ( 1 ), 60 – 70 . DOI: https://doi.org/10.1109/TITS.2006.884616
- Zhu, M. ; Wang, X. ; Wang, Y. Human-like autonomous car-following model with deep reinforcement learning . Transportation Research Part C: Emerging Technologies 2018 , 97 , 348 – 368 . DOI: https://doi.org/10.1016/j.trc.2018.10.024
- Zhou, M. ; Qu, X. ; Li, X. A recurrent neural network based microscopic car following model to predict traffic oscillation . Transportation Research Part C: Emerging Technologies 2017 , 84 , 245 – 264 . DOI: https://doi.org/10.1016/j.trc.2017.08.027
- Mo, Z. ; Shi, R. ; Di, X. A physics-informed deep learning paradigm for car-following models . Transportation Research Part C: Emerging Technologies 2021 , 130 , 103240 . DOI: https://doi.org/10.1016/j.trc.2021.103240
- Brackstone, M. ; McDonald, M. Car-following: a historical review . Transportation Research Part F: Traffic Psychology and Behaviour 1999 , 2 ( 4 ), 181 – 196 . DOI: https://doi.org/10.1016/S1369-8478(00)00005-X
- Chen, X.M. Stochastic evolutions of dynamic traffic flow: Modelling and application . Thesis, Ph.D. ,Department of Civil Engineering,Tsinghua University,Beijing,China , 2012 .
- Reuschel, A. Fahrzeugbewegungen in der Kolonne . Osterreichisches Ingenieur Archiv 1950 , 4 , 193 – 215 .
- Pipes, L.A. An operational analysis of traffic dynamics . Journal of Applied Physics 1953 , 24 ( 3 ), 274 – 281 . DOI: https://doi.org/10.1063/1.1721265
- Zhang, Y. ; Ni, P. ; Li, M. ; et al . A new car-following model considering driving characteristics and preceding vehicle’s acceleration . Journal of Advanced Transportation 2017 , 2017 , 2437539 . DOI: https://doi.org/10.1155/2017/2437539
- Gazis, D.C. ; Herman, R. ; Rothery, R.W. Nonlinear follow-the-leader models of traffic flow . Operations Research 1961 , 9 ( 4 ), 545 – 567 . DOI: https://doi.org/10.1287/opre.9.4.545
- Siuhi, S. ; Kaseko, M. Parametric study of stimulus-response behavior for car-following models . Paper 10 - 1179 . In The 89th Annual Meeting of the Transportation Research Board Compendium of Papers. 2010 . Available Online: https://trid.trb.org/view/910163 (Accessed on 12 June 2023).
- Siuhi, S. Parametric study of stimulus-response behavior incorporating vehicle heterogeneity in car-following models . thesis, Ph.D. ,University of Nevada, Vegas, Las ,NV,USA , 2009 .
- Newell, G.F. Nonlinear effects in the dynamics of car following . Operations Research 1961 , 9 ( 2 ), 209 – 229 . DOI: https://doi.org/10.1287/opre.9.2.209
- Saifuzzaman, M. Incorporating risk taking and driver errors in car-following models . thesis, Ph.D. ,Queensland University of Technology,Brisbane,Australia , 2016 .
- Gipps, P.G. A behavioural car-following model for computer simulation . Transportation Research Part B: Methodological 1981 , 15 ( 2 ), 105 – 111 . DOI: https://doi.org/10.1016/0191-2615(81)90037-0
- Punzo, V. ; Simonelli, F. Analysis and comparison of microscopic traffic flow models with real traffic microscopic data . Transportation Research Record 2005 , 1934 ( 1 ), 53 – 63 . DOI: https://doi.org/10.1177/0361198105193400106
- Punzo, V. ; Tripodi, A. Steady-state solutions and multiclass calibration of Gipps microscopic traffic flow model . Transportation Research Record 2007 , 1999 ( 1 ), 104 – 114 . DOI: https://doi.org/10.3141/1999-12
- Bando, M. ; Hasebe, K. ; Nakayama, A. ; et al . Dynamical model of traffic congestion and numerical simulation . Physical Review E 1995 , 51 ( 2 ), 1035 . DOI: https://doi.org/10.1103/PhysRevE.51.1035
- Zhao, H. ; He, R. ; Ma, C. An extended car-following model at signalised intersections . Journal of Advanced Transportation 2018 , 2018 , 5427507 . DOI: https://doi.org/10.1155/2018/5427507
- Helbing, D. ; Tilch, B. Generalized force model of traffic dynamics . Physical review E 1998 , 58 ( 1 ), 133 . DOI: https://doi.org/10.1103/PhysRevE.58.133
- Jiang, R. ; Wu, Q. ; Zhu, Z. Full velocity difference model for a car-following theory . Physical Review E 2001 , 64 ( 1 ), 017101 . DOI: https://doi.org/10.1103/PhysRevE.64.017101
- Bierley, R.L. Investigation of an intervehicle spacing display . Highway Research Record 1963 , ( 25 ). Available Online: https://trid.trb.org/view/111048 (Accessed on 12 June 2023).
- Leutzbach, W. ; Wiedemann, R. Development and applications of traffic simulation models at the Karlsruhe Institut fur Verkehrwesen . Traffic Engineering & Control 1986 , 27 ( 5 ), 270 – 278 .
- Sultan, B. ; Brackstone, M. ; McDonald, M. Drivers' use of deceleration and acceleration information in car-following process . Transportation Research Record 2004 , 1883 ( 1 ), 31 – 39 . DOI: https://doi.org/10.3141/1883-04
- Kesting, A. ; Treiber, M. ; Helbing, D. Enhanced intelligent driver model to access the impact of driving strategies on traffic capacity . Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2010 , 368 ( 1928 ), 4585 – 4605 . DOI: https://doi.org/10.1098/rsta.2010.0084
- Searle, J. Equations for speed, time and distance for vehicles under maximum acceleration . SAE Technical Paper 1999 , No. 1999-01-00 78 . DOI: https://doi.org/10.4271/1999-01-0078
- Rakha, H. ; Lucic, I. ; Demarchi, S.H. ; et al . Vehicle dynamics model for predicting maximum truck acceleration levels . Journal of Transportation Engineering 2001 , 127 ( 5 ), 418 – 425 . DOI: https://doi.org/10.1061/(ASCE)0733-947X(2001)127:5(418)
- Rakha, H. ; Lucic, I. Variable power vehicle dynamics model for estimating truck accelerations . Journal of Transportation Engineering 2002 , 128 ( 5 ), 412 – 419 . DOI: https://doi.org/10.1061/(ASCE)0733-947X(2002)128:5(412)
- Rakha, H. ; Snare, M. ; Dion, F. Vehicle dynamics model for estimating maximum light-duty vehicle acceleration levels . Transportation Research Record 2004 , 1883 ( 1 ), 40 – 49 . DOI: https://doi.org/10.3141/1883-05
- Rakha, H. Validation of Van Aerde's simplified steadystate car-following and traffic stream model . Transportation Letters 2009 , 1 ( 3 ), 227 – 244 . DOI: https://doi.org/10.3328/TL.2009.01.03.227-244
- Rakha, H.A. ; Ahn, K. ; Faris, W. ; et al . Simple vehicle powertrain model for modeling intelligent vehicle applications . IEEE Transactions on Intelligent Transportation Systems 2012 , 13 ( 2 ), 770 – 780 . DOI: https://doi.org/10.1109/TITS.2012.2188517
- Fadhloun, K. ; Rakha, H. ; Loulizi, A. ; et al . Vehicle dynamics model for estimating typical vehicle accelerations . Transportation Research Record 2015 , 2491 ( 1 ), 61 – 71 . DOI: https://doi.org/10.3141/2491-07
- Fadhloun, K. ; Rakha, H. A novel vehicle dynamics and human behavior car-following model: Model development and preliminary testing . International Journal of Transportation Science and Technology 2020 , 9 ( 1 ), 14 – 28 . DOI: https://doi.org/10.1016/j.ijtst.2019.05.004
- Stanton, N.A. ; Salmon, P.M. Human error taxonomies applied to driving: A generic driver error taxonomy and its implications for intelligent transport systems . Safety Science 2009 , 47 ( 2 ), 227 – 237 . DOI: https://doi.org/10.1016/j.ssci.2008.03.006
- Wiedemann, R. Simulation des StraBenverkehrsflusses . Institut fur Verkehrswesen .University of Karlsruhe,Germany , 1974 .
- Fritzsche, H.T. ; Ag, D.B. A model for traffic simulation . Traffic Engineering Control 1994 , 35 ( 5 ), 317 – 321 .
- Andersen, G.J. ; Sauer, C.W. Optical information for car following: The driving by visual angle (DVA) model . Human Factors 2007 , 49 ( 5 ), 878 – 896 . DOI: https://doi.org/10.1518/001872007X230235
- Jin, S. ; Wang, D.H. ; Huang, Z.Y. ; et al . Visual angle model for car-following theory . Physica A: Statistical Mechanics and Its Applications 2011 , 390 ( 11 ), 1931 – 1940 . DOI: https://doi.org/10.1016/j.physa.2011.01.012
- Hamdar, S.H. ; Treiber, M. ; Mahmassani, H.S. ; et al . Modeling driver behavior as sequential risk-taking task . Transportation Research Record 2008 , 2088 ( 1 ), 208 – 217 . DOI: https://doi.org/10.3141/2088-22
- Van Winsum, W. The human element in car following models . Transportation Research Part F: Traffic Psychology and Behaviour 1999 , 2 ( 4 ), 207 – 211 . DOI: https://doi.org/10.1016/S1369-8478(00)00008-5
- Yang, H.H. ; Peng, H. Development of an errorable car-following driver model . Vehicle System Dynamics 2010 , 48 ( 6 ), 751 – 773 . DOI: https://doi.org/10.1080/00423110903128524
- Fellendorf, M. ; Vortisch, P. Microscopic traffic flow simulator VISSIM . Fundamentals of traffic simulation 2010 , 145 , 63 – 93 . DOI: https://doi.org/10.1007/978-1-4419-6142-6_2
- Park, B. ; Qi, H. Microscopic simulation model calibration and validation for freeway work zone network-a case study of VISSIM . In 2006 IEEE Intelligent Transportation Systems Conference . IEEE : Piscataway, NJ, USA , 2006 , pp. 1471 – 1476 .
- Gomes, G. ; May, A. ; Horowitz, R. Calibration of VISSIM for a Congested Freeway . UC Berkeley : California Partners for Advanced Transportation Technology , 2004 . Available Online : https://escholarship.org/uc/item/7bs9b2v3 (Accessed on 12 June 2023).
- Michaels, R.M. Perceptual factors in car-following . Proc. of 2nd ISTTF (London) 1963 , 44 – 59 .
- Gray, R. ; Regan, D. Accuracy of estimating time to collision using binocular and monocular information . Vision Research 1998 , 38 ( 4 ), 499 – 512 . DOI: https://doi.org/10.1016/S0042-6989(97)00230-7
- Helly, W. Simulation of bottlenecks in single-lane traffic flow . 1959 . Available Online: https://trid.trb.org/view/115225 (Accessed on 12 June 2023).
- Von Neumann, J. ; Morgenstern, O. Theory of games and economic behavior . In Theory of Games and Economic Behavior . Princeton University Press : Princeton, NJ, USA , 2007 .
- Kahneman, D. ; Tversky, A. Prospect theory: An analysis of decision under risk . Econometrica 1979 , 47 ( 2 ), 363 – 391 . DOI: https://doi.org/10.2307/1914185
- Hamdar, S.H. ; Mahmassani, H.S. ; Treiber, M. From behavioral psychology to acceleration modeling: Calibration, validation, and exploration of drivers’ cognitive and safety parameters in a risk-taking environment . Transportation Research Part B: Methodological 2015 , 78 , 32 – 53 . DOI: https://doi.org/10.1016/j.trb.2015.03.011
- Reason, Human Error, J. . Cambridge university press: Cambridge , UK , 1990 .
- Parker, D. ; Reason, J.T. ; Manstead, A.S. ; et al . Driving errors, driving violations and accident involvement . Ergonomics 1995 , 38 ( 5 ), 1036 – 1048 . DOI: https://doi.org/10.1080/00140139508925170
- Di, X. ; Shi, R. A survey on autonomous vehicle control in the era of mixed-autonomy: From physics-based to AI-guided driving policy learning . Transportation Research Part C: Emerging Technologies 2021 , 125 , 103008 . DOI: https://doi.org/10.1016/j.trc.2021.103008
- Wei, D. ; Liu, H. Analysis of asymmetric driving behavior using a self-learning approach . Transportation Research Part B: Methodological 2013 , 47 , 1 – 14 . DOI: https://doi.org/10.1016/j.trb.2012.09.003
- Huang, X. ; Sun, J. ; Sun, J. A car-following model considering asymmetric driving behavior based on long short-term memory neural networks . Transportation Research Part C: Emerging Technologies 2018 , 95 , 346 – 362 . DOI: https://doi.org/10.1016/j.trc.2018.07.022
- Gu, Z. ; Li, Z. ; Di, X. ; et al . An LSTM-based autonomous driving model using a waymo open dataset . Applied Sciences 2020 , 10 ( 6 ), 2046 . DOI: https://doi.org/10.3390/app10062046
- He, Z. ; Zheng, L. ; Guan, W. A simple nonparametric car-following model driven by field data . Transportation Research Part B: Methodological 2015 , 80 , 185 – 201 . DOI: https://doi.org/10.1016/j.trb.2015.07.010
- Kuefler, A. ; Morton, J. ; Wheeler, T. ; et al . Imitating driver behavior with generative adversarial networks . In 2017 IEEE Intelligent Vehicles Symposium (IV) . IEEE : Piscataway, NJ, USA , 2017 , pp. 204 – 211 .
- Zhou, Y. ; Fu, R. ; Wang, C. ; et al . Modeling Car-Following Behaviors and Driving Styles with Generative Adversarial Imitation Learning . Sensors 2020 , 20 , 5034 . DOI: https://doi.org/10.3390/s20185034
- Yang, D. ; Zhu, L. ; Liu, Y. ; et al . A novel car-following control model combining machine learning and kinematics models for automated vehicles . IEEE Transactions on Intelligent Transportation Systems 2018 , 20 ( 6 ), 1991 – 2000 . DOI: https://doi.org/10.1109/TITS.2018.2854827
- Yuan, Y. ; Wang, Q. ; Yang, X.T. Modeling stochastic microscopic traffic behaviors: a physics regularized Gaussian process approach . arXiv Preprint 2020 , arXiv: 2007.10109 .
- Shou, Z. ; Wang, Z. ; Han, K. ; et al . Long-term prediction of lane change maneuver through a multilayer perceptron . In 2020 IEEE Intelligent Vehicles Symposium (IV) . IEEE : Piscataway, NJ, USA , 2020 , pp. 246 – 252 .






