The large-scale flexible job shop dynamic scheduling problem (LSFJSDSP) has a more complex solution space than the original job shop problem because of the increase in the number of jobs and machines, which makes the traditional solution algorithm unable to meet the actual production requirements in terms of the solution quality and time. To address this problem, we develop a dynamic scheduling model of a large-scale flexible job shop based on noisynet-double deep Q-networks (N-DDQNs), which takes the minimum expected completion time as the optimization objective and thoroughly takes into account the two dynamic factors (the new job arrival and the stochastic processing time). Firstly, a Markov decision process model is constructed for dynamic scheduling of a large-scale flexible workshop, and the corresponding reasonable state space, action space and reward function are designed. To address the problems (of solution stability and unsatisfactory scheduling strategy selection) in the conventional exploration method of DDQNs, learnable noise parameters are added to the DDQNs to create the N-DDQN algorithm framework, where the uncertainty weight is added. Secondly, the learnable noise parameters are added to the DDQNs to form the N-DDQN algorithm framework, and the uncertainty weight is added to realize automatic exploration. Hence, the issue is solved that the traditional DDQN exploration method may result in unsatisfactory solution stability and scheduling strategy selection. The proposed method, which has significant flexibility and efficacy, is demonstrated (by experimental findings) to be superior to the conventional method based on compound scheduling rules in tackling large-scale flexible job shop dynamic scheduling problems.
- Open Access
- Article
Dynamic Scheduling for Large-Scale Flexible Job Shop Based on Noisy DDQN
- Tingjuan Zheng 1, 2,
- Yongbing Zhou 1,
- Mingzhu Hu 1,
- Jian Zhang 1, *
Author Information
Received: 03 Jul 2023 | Accepted: 08 Oct 2023 | Published: 21 Dec 2023
Abstract
Graphical Abstract
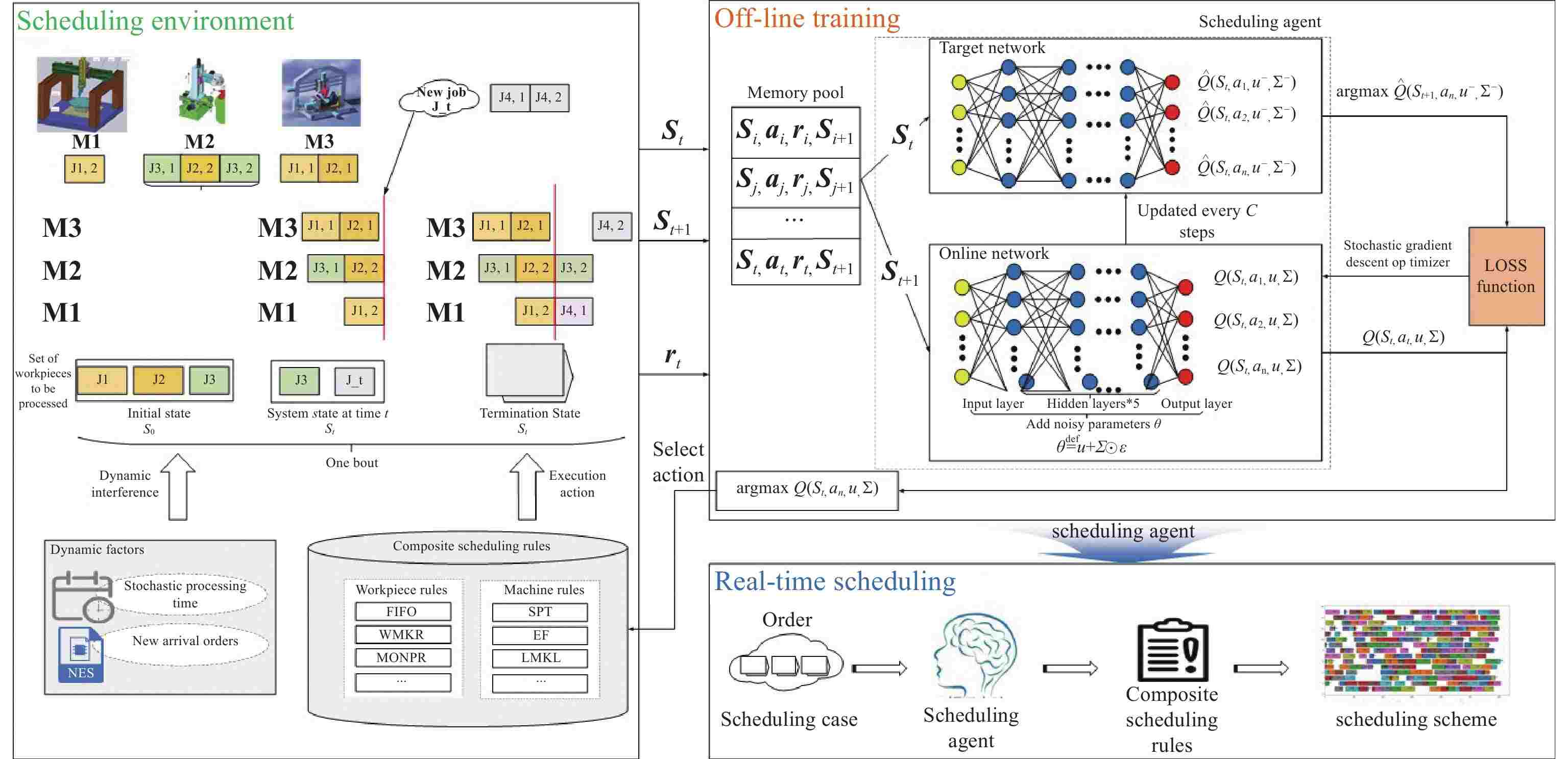
Keywords
large-scale flexible job shop | dynamic scheduling | new job arrival | stochastic processing time | deep reinforcement learning
References
- 1.Lu, C.; Li, X.Y.; Gao, L.; et al. An effective multi-objective discrete virus optimization algorithm for flexible job-shop scheduling problem with controllable processing times. Comput. Ind. Eng., 2017, 104: 156−174. doi: 10.1016/j.cie.2016.12.020
- 2.Caldeira, R.H.; Gnanavelbabu, A.; Vaidyanathan, T. An effective backtracking search algorithm for multi-objective flexible job shop scheduling considering new job arrivals and energy consumption. Comput. Ind. Eng., 2020, 149: 106863. doi: 10.1016/j.cie.2020.106863
- 3.Gao, K.Z.; Suganthan, P.N.; Tasgetiren, M.F.; et al. Effective ensembles of heuristics for scheduling flexible job shop problem with new job insertion. Comput. Ind. Eng., 2015, 90: 107−117. doi: 10.1016/j.cie.2015.09.005
- 4.Long, X.J.; Zhang, J.T.; Zhou, K.; et al. Dynamic self-learning artificial bee colony optimization algorithm for flexible job-shop scheduling problem with job insertion. Processes, 2022, 10: 571. doi: 10.3390/pr10030571
- 5.Gao, K.Z.; Suganthan, P.N.; Pan, Q. K; et al. An effective discrete harmony search algorithm for flexible job shop scheduling problem with fuzzy processing time. Int. J. Prod. Res., 2015, 53: 5896−5911. doi: 10.1080/00207543.2015.1020174
- 6.Mokhtari, H.; Dadgar, M. Scheduling optimization of a stochastic flexible job-shop system with time-varying machine failure rate. Comput. Oper. Res., 2015, 61: 31−45. doi: 10.1016/j.cor.2015.02.014
- 7.Yang, X.; Zeng, Z.X.; Wang, R.D.; et al. Bi-objective flexible job-shop scheduling problem considering energy consumption under stochastic processing times. PLoS One, 2016, 11: e0167427. doi: 10.1371/journal.pone.0167427
- 8.Shen, X.N.; Han, Y.; and Fu, J. Z. Robustness measures and robust scheduling for multi-objective stochastic flexible job shop scheduling problems. Soft Comput., 2017, 21: 6531−6554. doi: 10.1007/s00500-016-2245-4
- 9.Zhang, J.; Ding, G.F.; Zou, Y.S.; et al. Review of job shop scheduling research and its new perspectives under industry 4.0. J. Intell. Manuf., 2019, 30: 1809−1830. doi: 10.1007/s10845-017-1350-2
- 10.Van Den Akker, J.M.; Hurkens, C.A.J.; Savelsbergh, M.W.P. Time-indexed formulations for machine scheduling problems: Column generation. INFORMS J. Comput., 2000, 12: 111−124. doi: 10.1287/ijoc.12.2.111.11896
- 11.Liu, M.; Hao, J.H.; Wu, C. A prediction based iterative decomposition algorithm for scheduling large-scale job shops. Math. Comput. Modell., 2008, 47: 411−421. doi: 10.1016/j.mcm.2007.03.032
- 12.Luo, S.; Zhang, L.X.; Fan, Y. S. Dynamic multi-objective scheduling for flexible job shop by deep reinforcement learning. Comput. Ind. Eng., 2021, 159: 107489. doi: 10.1016/j.cie.2021.107489
- 13.Luo, S. Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning. Appl. Soft Comput., 2020, 91: 106208. doi: 10.1016/j.asoc.2020.106208
- 14.Gui, Y.; Tang, D.B.; Zhu, H.H.; et al. Dynamic scheduling for flexible job shop using a deep reinforcement learning approach. Comput. Ind. Eng., 2023, 180: 109255. doi: 10.1016/j.cie.2023.109255
- 15.Waschneck, B.; Reichstaller, A.; Belzner, L.; et al. Optimization of global production scheduling with deep reinforcement learning. Procedia CIRP, 2018, 72: 1264−1269. doi: 10.1016/j.procir.2018.03.212
- 16.Song, W.; Chen, X.Y.; Li, Q.Q.; et al. Flexible job-shop scheduling via graph neural network and deep reinforcement learning. IEEE Trans. Ind. Inf., 2023, 19: 1600−1610. doi: 10.1109/TⅡ.2022.3189725
- 17.Park, I.B.; Park, J. Scalable scheduling of semiconductor packaging facilities using deep reinforcement learning. IEEE Trans. Cybern., 2023, 53: 3518−3531. doi: 10.1109/TCYB.2021.3128075
- 18.Mnih, V.; Kavukcuoglu, K.; Silver, D.; et al. Human-level control through deep reinforcement learning. Nature, 2015, 518: 529−533. doi: 10.1038/nature14236
- 19.Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-learning. In
Proceedings of the 30th AAAI Conference on Artificial Intelligence ,Phoenix ,Arizona ,USA ,12 –17 February 2016 ; AAAI Press: Phoenix, 2015; pp. 2094–2100. - 20.Fortunato, M.; Azar, M.G.; Piot, B.;
et al . Noisy networks for exploration. InProceedings of the 6th International Conference on Learning Representations ,Vancouver ,BC ,Canada ,30 April – 3 May ,2018 ; OpenReview.net: Vancouver, 2018. - 21.Ghoshal, B.; Tucker, A. Hyperspherical weight uncertainty in neural networks. In
Proceedings of the 19th International Symposium on Intelligent Data Analysis XIX ,Porto ,Portugal ,26 – 28 April 2021 ; Springer: Porto, 2021; pp. 3–11. - 22.Durasević, M.; Jakobović, D. A survey of dispatching rules for the dynamic unrelated machines environment. Expert Syst. Appl., 2018, 113: 555−569. doi: 10.1016/j.eswa.2018.06.053
- 23.Han, B.A.; Yang, J. J. Research on adaptive job shop scheduling problems based on dueling double DQN. IEEE Access, 2020, 8: 186474−186495. doi: 10.1109/ACCESS.2020.3029868
- 24.Pandey, M. How to decide the number of hidden layers and nodes in a hidden layer? 2023.
How to Cite
Zheng, T.; Zhou, Y.; Hu, M.; Zhang, J. Dynamic Scheduling for Large-Scale Flexible Job Shop Based on Noisy DDQN. International Journal of Network Dynamics and Intelligence 2023, 2 (4), 100015. https://doi.org/10.53941/ijndi.2023.100015.
RIS
BibTex
Copyright & License

Copyright (c) 2023 by the authors.
This work is licensed under a Creative Commons Attribution 4.0 International License.
Contents
References


