Non-Gaussian randomness widely exists in complex dynamical systems, in which the traditional mean-variance index cannot fully reflect the systematic characteristics. To improve the performance of control design subjected to non-Gaussian noises, stochastic distribution control (SDC) theory was proposed in the 1990s, where the output probability density function (PDF) has been investigated as an additional system variable. Following this framework, SDC has been extended to other research subjects in control systems such as filter design, fault diagnosis, and so on. It shows that SDC supplies an important solution to enhance the accuracy of system design, which is further beneficial to almost all the topics subject to non-Gaussian randomness. Meanwhile, the theoretical results of the SDC have been applied to several practical industrial applications. As data science raises based on the development of industrial artificial intelligence, SDC has been further developed recently focusing on data-driven design and multi-agent systems. To explore the new challenges with the evolution of SDC, e.g. unknown system models, unknown noise distributions, strong non-stationary transient dynamics, stability analysis and industrial applications, this survey summarises the most recent published results in the last 5 years of SDC work in terms of modelling, control, filtering, fault diagnosis, and industrial applications. Based on the technical analysis, potential future work is discussed in the end.
- Open Access
- Survey/Review Study
Recent Advances in Non-Gaussian Stochastic Systems Control Theory and Its Applications
- Qichun Zhang 1,
- Yuyang Zhou 2, *
Author Information
Received: 24 Oct 2022 | Accepted: 18 Nov 2022 | Published: 22 Dec 2022
Abstract
Graphical Abstract
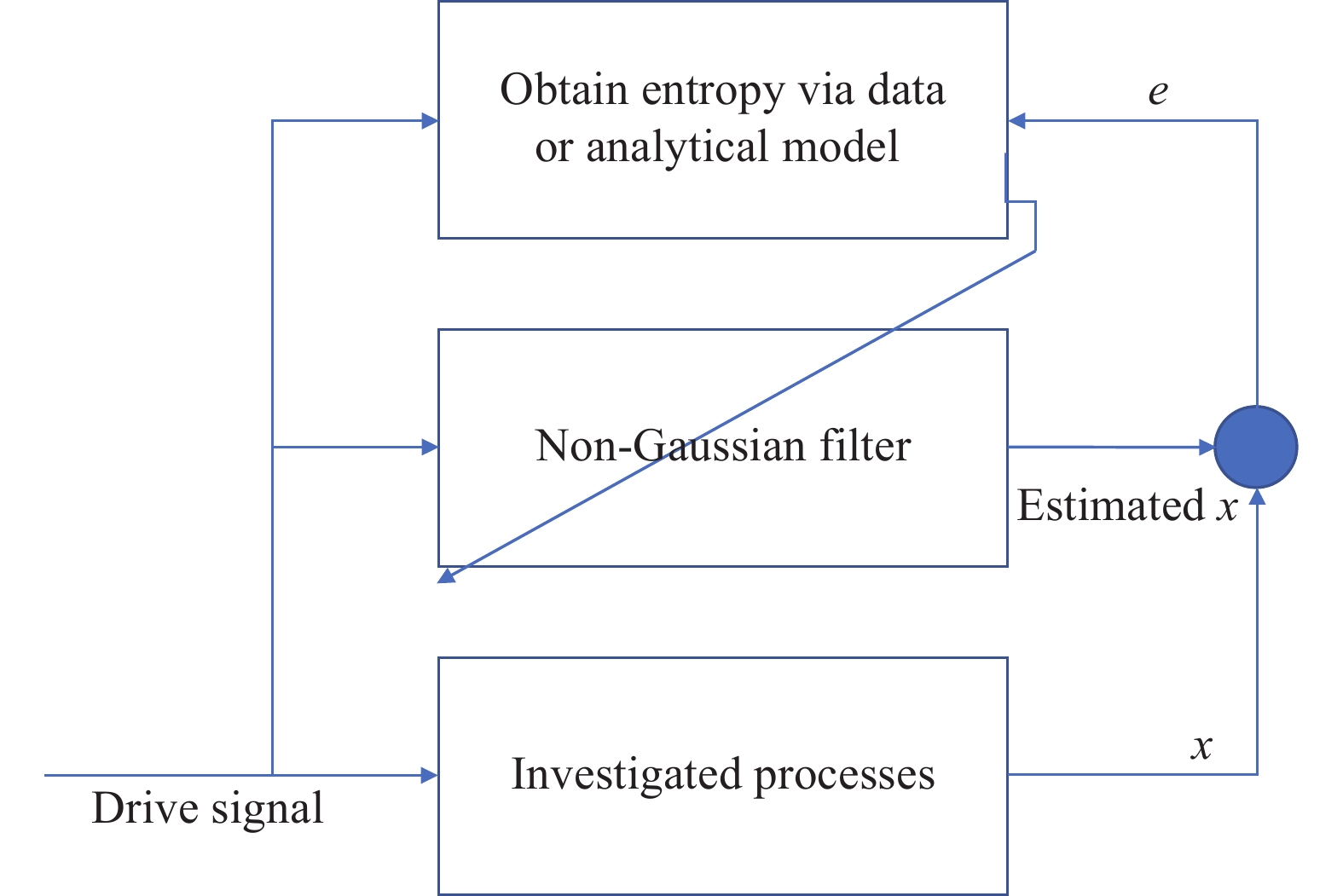
Keywords
stochastic distribution control | minimum entropy control | minimum entropy filtering | full probabilistic design | data-driven design | fault diagnosis | performance enhancement | non-gaussian stochastic systems
References
- 1.Ren, M.F.; Zhang, Q.C.; Zhang, J.H, An introductory survey of probability density function control. Syst. Sci. Control Eng., 2019, 7: 158−170.
- 2.Wang, A.P.; Wang, H, Survey on stochastic distribution systems: A full probability density function control theory with potential applications. Opt. Control Appl. Methods, 2021, 42: 1812−1839.
- 3.Herzallah, R, A fully probabilistic design for tracking control for stochastic systems with input delay. IEEE Trans. Autom. Control, 2021, 66: 4342−4348.
- 4.Herzallah, R, A fully probabilistic design for stochastic systems with input delay. Int. J. Control, 2021, 94: 2934−2944.
- 5.Herzallah, R.; Zhou, Y.Y, A fully probabilistic control framework for stochastic systems with input and state delay. Sci. Rep., 2022, 12: 7812.
- 6.Herzallah, R.; Zhou, Y.Y, A tracking error–based fully probabilistic control for stochastic discrete-time systems with multiplicative noise. J. Vib. Control, 2020, 26: 2329−2339.
- 7.Zhou, Y.Y.; Herzallah, R, DOBC based fully probability design for stochastic system with the multiplicative noise. IEEE Access, 2020, 8: 34225−34235.
- 8.Herzallah, R.; Zhou, Y.Y. An efficient message passing algorithm for decentrally controlling complex systems.
Int .J .Control 2021 , in press. doi:10.1080/00207179.2021.2011422 - 9.Zhou, Y.Y.; Herzallah, R, Probabilistic message passing control and FPD based decentralised control for stochastic complex systems. AIMS Electron. Electr. Eng., 2020, 4: 216−233.
- 10.Zhou, Y.Y.; Herzallah, R, Probabilistic message passing control for complex stochastic switching systems. J. Franklin Inst., 2021, 358: 5451−5469.
- 11.Lai, L.L.; Yin, L.P.; Hong, Y.; et al, Data driven optimal control for stochastic systems with non-Gaussian disturbances. Int. J. Modell. Identif. Control, 2021, 39: 245−256.
- 12.Yin, L.P.; Wang, H.; Guo, L.; et al, Data-driven Pareto-DE-based intelligent optimal operational control for stochastic processes. IEEE Trans. Syst. Man Cybern. Syst., 2021, 51: 4443−4452.
- 13.Zhang, Q.C.; Wang, H, A novel data-based stochastic distribution control for non-Gaussian stochastic systems. IEEE Trans. Autom. Control, 2022, 67: 1506−1513.
- 14.Liu, Y.F.; Zhang, Q.C.; Yue, H, Stochastic distribution tracking control for stochastic non-linear systems via probability density function vectorisation. Trans. Inst. Meas. Control, 2021, 43: 3149−3157.
- 15.Zhang, Q.C.; Wang, H, Probability density function control for stochastic nonlinear systems using Monte Carlo simulation. IFAC-PapersOnLine, 2020, 53: 1288−1293.
- 16.Zhang, Q.C.; Zhang, J.H.; Wang, H. Data-driven minimum entropy control for stochastic nonlinear systems using the cumulant-generating function.
IEEE Trans .Autom .Control 2022 , in press. doi:10.1109/TAC.2022.3208170 - 17.Liu, Y.L.; Wang, A.P.; Guo, L.; et al, An error-entropy minimization algorithm for tracking control of nonlinear stochastic systems with non-Gaussian variables. IFAC-PapersOnLine, 2017, 50: 10407−10412.
- 18.Tian, B.; Wang, Y.; Guo, L, Disturbance observer-based minimum entropy control for a class of disturbed non-Gaussian stochastic systems. IEEE Trans. Cybern., 2020, 52: 4916−4925.
- 19.Zhang, J.H.; Pu, J.Z.; Lin, M.M.; et al, Superheating control of ORC systems via minimum (h,φ)-entropy control. Entropy, 2022, 24: 513.
- 20.Ren, M.F.; Gong, M.Y.; Lin, M.M.; et al, Generalized correntropy predictive control for waste heat recovery systems based on organic rankine cycle. IEEE Access, 2019, 7: 151587−151594.
- 21.Yin, L.P.; Lai, L.L.; Zhu, Z.J.; et al, Maximum power point tracking control for non-Gaussian wind energy conversion system by using survival information potential. Entropy, 2022, 24: 818.
- 22.Tian, B.; Wang, C.L.; Guo, L, Composite Antidisturbance control for non-Gaussian stochastic systems via information-theoretic learning technique. IEEE Trans. Neural Netw. Learn. Syst., 2022, 33: 7644−7654.
- 23.Zhang, Q.C.; Hu, L.; Gow, J, Output feedback stabilization for MIMO semi-linear stochastic systems with transient optimisation. Int. J. Autom. Comput., 2020, 17: 83−95.
- 24.Tang, X.F.; Zhou, Y.Y.; Zou, Y.Q.; et al, Variance and entropy assignment for continuous-time stochastic nonlinear systems. Entropy, 2022, 24: 25.
- 25.Li, W.S.; Wang, Z.D.; Yuan, Y.; et al, Two-stage particle filtering for non-Gaussian state estimation with fading measurements. Automatica, 2020, 115: 108882.
- 26.Li, W.S.; Guo, L, Robust particle filtering with time-varying model uncertainty and inaccurate noise covariance matrix. IEEE Trans. Syst. Man Cybern. Syst., 2021, 51: 7099−7108.
- 27.Yin, X.; Zhang, Q. C.; Wang, H.; et al, RBFNN-based minimum entropy filtering for a class of stochastic nonlinear systems. IEEE Trans. Autom. Control, 2020, 65: 376−381.
- 28.Yin, X.; Zhang, Q.C, Backstepping-based state estimation for a class of stochastic nonlinear systems. Complex Eng. Syst., 2022, 2: 1.
- 29.Zhang, Q.C, Performance enhanced Kalman filter design for non-Gaussian stochastic systems with data-based minimum entropy optimisation. AIMS Electron. Electr. Eng., 2019, 3: 382−396.
- 30.Gogineni, V.C.; Talebi, S.P.; Werner, S.; et al, Fractional-order correntropy adaptive filters for distributed processing of α-stable signals. IEEE Signal Process. Lett., 2020, 27: 1884−1888.
- 31.Gogineni, V.C.; Talebi, S.P.; Werner, S.; et al, Fractional-order correntropy filters for tracking dynamic systems in α-stable environments. IEEE Trans. Circuits Syst. II Exp. Briefs, 2020, 67: 3557−3561.
- 32.Alex, D.; Gogineni, V.C.; Mula, S.; et al, Novel VLSI architecture for fractional-order correntropy adaptive filtering algorithm. IEEE Trans. Very Large Scale Integr. VLSI Syst., 2022, 30: 893−904.
- 33.Fakoorian, S.; Izanloo, R.; Shamshirgaran, A.; et al. Maximum correntropy criterion Kalman filter with adaptive kernel size. In
Proceedings of 2019 IEEE National Aerospace and Electronics Conference ,Dayton ,OH ,USA ,15–19 July 2019 ; IEEE: Dayton, 2019; pp. 581–584. doi:10.1109/NAECON46414.2019.9057886 - 34.Zhang, T.; Wang, S.Y, Nyström kernel algorithm under generalized maximum correntropy criterion. IEEE Signal Process. Lett., 2020, 27: 1535−1539.
- 35.Zhao, J.; Zhang, H.B, Kernel recursive generalized maximum correntropy. IEEE Signal Process. Lett., 2017, 24: 1832−1836.
- 36.Zhao, H.Q.; Chen, B.; Zhu, Y.Y.; et al, Variable Kernel width algorithm of generalized maximum correntropy criteria for censored regression. IEEE Trans. Circuits Syst. II Exp. Briefs, 2021, 69: 1877−1881.
- 37.Sun, Q.; Zhang, H.; Wang, X.F.; et al, Sparsity constrained recursive generalized maximum correntropy criterion with variable center algorithm. IEEE Trans. Circuits Syst. II Exp. Briefs, 2020, 67: 3517−3521.
- 38.Zhao, J.; Zhang, J.A.; Li, Q.; et al, Recursive constrained generalized maximum correntropy algorithms for adaptive filtering. Signal Process., 2022, 199: 108611.
- 39.Liu, D.X.; Zhao, H.Q.; He, X.Q.; et al, Polynomial constraint generalized maximum correntropy normalized subband adaptive filter algorithm. Circuits Syst. Signal Process., 2022, 41: 2379−2396.
- 40.Zhu, Y.Y.; Zhao, H.Q.; Zeng, X.P.; et al, Robust generalized maximum correntropy criterion algorithms for active noise control. IEEE/ACM Trans. Audio Speech Lang. Process., 2020, 28: 1282−1292.
- 41.Bhattacharjee, S.S.; Shaikh, M.A.; Kumar, K.; et al, Robust constrained generalized correntropy and maximum versoria criterion adaptive filters. IEEE Trans. Circuits Syst. II Exp. Briefs, 2021, 68: 3002−3006.
- 42.Chen, F.; Li, X.Y.; Duan, S.K.; et al, Diffusion generalized maximum correntropy criterion algorithm for distributed estimation over multitask network. Digital Signal Process., 2018, 81: 16−25.
- 43.Sun, L.; Ho, W.K.; Ling, K.V.; et al, Recursive maximum likelihood estimation with t-distribution noise model. Automatica, 2021, 132: 109789.
- 44.Bai, M.M.; Sun, C.J.; Zhang, Y.G, A ROBUST GENeralized t distribution-based Kalman filter. IEEE Trans. Aerosp. Electron. Syst., 2022, 58: 4771−4781.
- 45.Yan, L.P.; Di, C.Y.; Wu, Q.M.J.; et al, Distributed fusion estimation for multisensor systems with non-Gaussian but heavy-tailed noises. ISA Trans., 2020, 101: 160−169.
- 46.Li, Q.; Ben, Y.Y.; Naqvi, S.M.; et al, Robust student’s t-based cooperative navigation for autonomous underwater vehicles. IEEE Trans. Instrum. Meas., 2018, 67: 1762−1777.
- 47.Youn, W.; Huang, Y.L.; Myung, H, Outlier-robust student's-t-based IMM-VB localization for manned aircraft using TDOA measurements. IEEE/ASME Trans. Mechatron., 2020, 25: 1646−1658.
- 48.Xu, C.; Zhao, S.Y.; Ma, Y.J.; et al, Robust filter design for asymmetric measurement noise using variational Bayesian inference. IET Control Theory Appl., 2019, 13: 1656−1664.
- 49.Zhang, T.Y.; Zhao, S.Y.; Luan, X.L.; et al. Bayesian inference for state-space models with student-
t mixture distributions.IEEE Trans .Cybern .2022 , in press. doi:10.1109/TCYB.2022.3183104 - 50.Jin, H.K.; Guan, Y.C.; Yao, L.N, Minimum entropy active fault tolerant control of the non-Gaussian stochastic distribution system subjected to mean constraint. Entropy, 2017, 19: 218.
- 51.Li, L.F.; Yao, L.N, Minimum rational entropy fault tolerant control for non-Gaussian singular stochastic distribution control systems using T-S fuzzy modelling. Int. J. Syst. Sci., 2018, 49: 2900−2911.
- 52.Yao, L.N.; Li, L.F.; Guan, Y.C.; et al, Fault diagnosis and fault-tolerant control for non-Gaussian nonlinear stochastic systems via entropy optimisation. Int. J. Syst. Sci., 2019, 50: 2552−2564.
- 53.Hu, K.Y.; Chen, F.Y.; Cheng, Z.A.; et al, Adaptive minimum-entropy hybrid compensation for compound faults of non-Gaussian stochastic systems. IEEE Access, 2019, 7: 120695−120707.
- 54.Xu, X.Y.; Zhang, Y.Y.; Ren, M.F.; et al, Generalized correntropy filter-based fault diagnosis and tolerant control for non-Gaussian stochastic systems subject to sensor faults. IEEE Access, 2018, 6: 12598−12607.
- 55.Yin, L.P.; Zhu, P.W.; Li, T, Fault detection and diagnosis for delay-range-dependent stochastic systems using output PDFs. Int. J. Control Autom. Syst., 2017, 15: 1701−1709.
- 56.Zhou, J.L.; Jia, Y.Q.; Jiang, H.X.; et al, Non-Gaussian systems control performance assessment based on rational entropy. Entropy, 2018, 20: 331.
- 57.Tang, X.F.; Zhang, Q.C.; Hu, L, An EKF-based performance enhancement scheme for stochastic nonlinear systems by dynamic set-point adjustment. IEEE Access, 2020, 8: 62261−62272.
- 58.Zhang, Q.C.; Yin, X, Observer-based parametric decoupling controller design for a class of multi-variable non-linear uncertain systems. Syst. Sci. Control Eng., 2018, 6: 258−267.
- 59.Zhou, Y.Y.; Wang, A.P.; Zhou, P.; et al, Dynamic performance enhancement for nonlinear stochastic systems using RBF driven nonlinear compensation with extended Kalman filter. Automatica, 2020, 112: 108693.
- 60.Zhang, J.H.; Pu, J.Z.; Ren, M.F, Molecular weight distribution control for polymerization processes based on the moment-generating function. Entropy, 2022, 24: 499.
- 61.Herzallah, R.; Zhou, Y.Y, Probabilistic decentralised control and message passing framework for future grid. Int. J. Electr. Power Energy Syst., 2021, 131: 107114.
- 62.Zhang, Y.; Zhou, P.; Cui, G.M, Multi-model based PSO method for burden distribution matrix optimization with expected burden distribution output behaviors. IEEE/CAA J. Autom. Sin., 2019, 6: 1506−1512.
- 63.Zhang, Y.; Zhou, P.; Lv, D.H.; et al, Inverse calculation of burden distribution matrix using B-spline model based PDF control in blast furnace burden charging process. IEEE Trans. Ind. Inf., 2023, 19: 317−327.
- 64.Li, M.J.; Zhou, P.; Liu, Y.L.; et al. Data-driven predictive probability density function control of fiber length stochastic distribution shaping in refining process. IEEE Trans. Automat. Sci. Eng. 2020, 17, 633–645. doi:10.1109/TASE.2019.2939052
- 65.Tang, X.F.; Zhang, Q.C.; Dai, X.W.; et al, Neural membrane mutual coupling characterisation using entropy-based iterative learning identification. IEEE Access, 2020, 8: 205231−205243.
- 66.Zhang, X.M.; Han, Q.L.; Ge, X.H.; et al, Networked control systems: A survey of trends and techniques. IEEE/CAA J. Autom. Sin., 2020, 7: 1−17.
- 67.Pratama, M.; Wang, D.H, Deep stacked stochastic configuration networks for lifelong learning of non-stationary data streams. Inf. Sci., 2019, 495: 150−174.
- 68.Zhang, D.D.; Si, W.Y.; Fan, W.; et al, From teleoperation to autonomous robot-assisted microsurgery: A survey. Mach. Intell. Res., 2022, 19: 288−306.
How to Cite
Zhang, Q.; Zhou, Y. Recent Advances in Non-Gaussian Stochastic Systems Control Theory and Its Applications. International Journal of Network Dynamics and Intelligence 2022, 1 (1), 111–119. https://doi.org/10.53941/ijndi0101010.
RIS
BibTex
Copyright & License

Copyright (c) 2022 by the authors.
This work is licensed under a Creative Commons Attribution 4.0 International License.
Contents
References


