Unknown correlations (UCs) generally exist in a wide spectrum of practical multi-source information fusion problems, and thereby, their corresponding fusion problems have become one of the most important topics in information fusion domain. During the past three decades, the research on this topic has been growing rapidly and extensively, and, as a result, various important advances have been reported. In this overview, we intend to summarize the culmination of years of development in the field of information fusion under UCs as a roadmap. First, the potential reasons leading to UCs are investigated. According to the unknown nature of correlations, we further divide UCs into two categories, i.e., fully UCs, and partially UCs. For each category, the corresponding fusion methods are reviewed. Next, this roadmap witnesses the recent development of information fusion under UCs in a distributed way thanks to the popularity of distributed sensing technology. In particular, the distributed fusion techniques based on consensus, diffusion, and multi-object tracking strategies for UCs are examined. Finally, some future perspectives on information fusion under UCs are pointed out.
- Open Access
- Survey/Review Study
Information Fusion over Network Dynamics with Unknown Correlations: An Overview
- Wangyan Li 1,
- Fuwen Yang 2, *
Author Information
Received: 24 Oct 2022 | Accepted: 22 Nov 2022 | Published: 23 Jun 2023
Abstract
Graphical Abstract
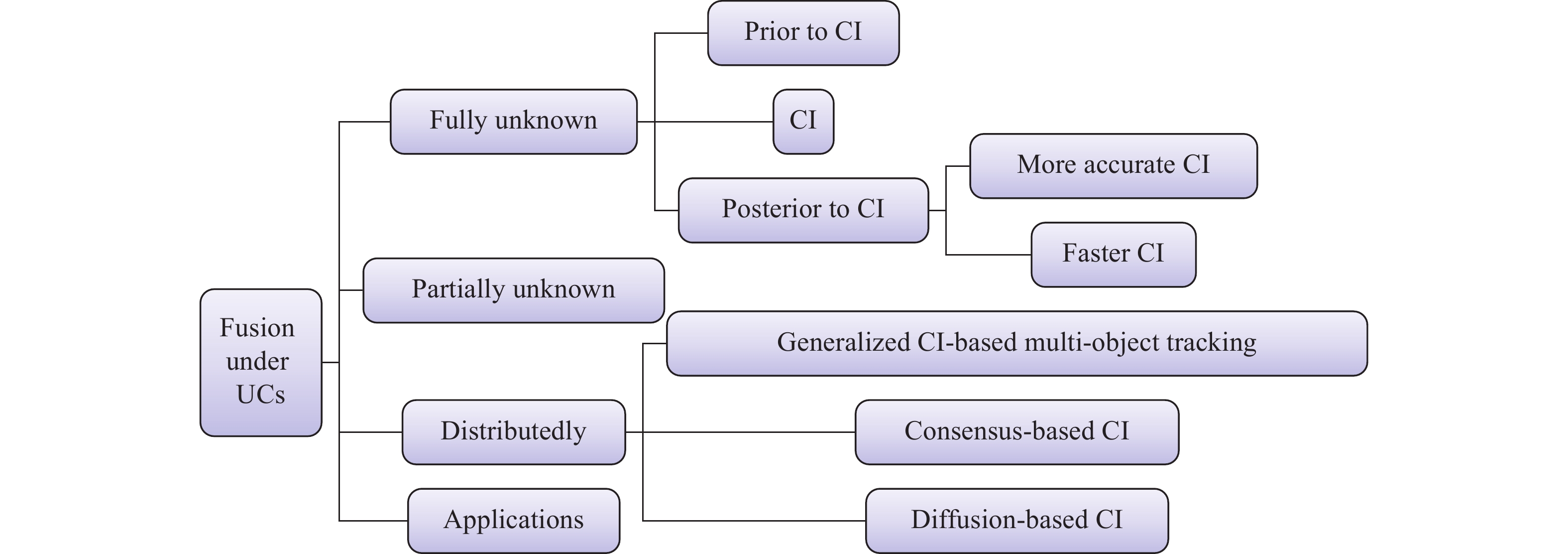
Keywords
unknown correlations | partially unknown correlations | multi-sensor fusion | diffusion | consensus | covariance intersection
References
- 1.Hall, D.L.; Llinas, J. An introduction to multisensor data fusion. Proc. IEEE, 1997, 85: 6−23.
- 2.Chen, L.J.; Arambel, P.O.; Mehra, R.K. Estimation under unknown correlation: Covariance intersection revisited. IEEE Trans. Autom. Control, 2002, 47: 1879−1882.
- 3.Reinhardt, M.; Noack, B.; Arambel, P.O.; et al. Minimum covariance bounds for the fusionunder unknown correlations. IEEE Signal Process. Lett., 2015, 22: 1210−1214.
- 4.Bar-Shalom, Y.; Campo, L. The effect of the common process noise on the two-sensor fused-track covariance. IEEE Trans. Aerosp. Electron. Syst. 1986, AES-22, 803–805. doi: 10.1109/TAES.1986.310815.
- 5.Julier, S.J.; Uhlmann, J.K. A non-divergent estimation algorithm in the presence of unknown correlations. In Proceedings of the 16th American Control Conference, Albuquerque, 06 June 1997; IEEE: Albuquerque, 1997; pp. 2369–2373. doi: 10.1109/ACC.1997.609105.
- 6.Wang, Y.M.; Li, X.R. Distributed estimation fusion with unavailable cross-correlation. IEEE Trans. Aerosp. Electron. Syst., 2012, 48: 259−278.
- 7.Uhlmann, J.K. General data fusion for estimates with unknown cross covariances. In Proceedings of SPIE 2755, Signal Processing, Sensor Fusion, and Target Recognition V, Orlando, 14 June 1996; SPIE: Orlando, 1996; p. 2755. doi: 10.1117/12.243195.
- 8.Li, W.Y.; Wang, Z.D.; Wei, G.L.; et al. A survey on multi-sensor fusion and consensus filtering for sensor networks. Discrete Dyn. Nat. Soc., 2015, 2015: 683701.
- 9.Gao, Y.X.; Li, X.R.; Song, E.B. Robust linear estimation fusion with allowable unknown cross-covariance. IEEE Trans. Syst. Man Cybernet. Syst., 2016, 46: 1314−1325.
- 10.Wu, Z.Z.; Cai, Q.Q.; Fu, M.Y. Covariance intersection for partially correlated random vectors. IEEE Trans. Automat. Control, 2018, 63: 619−629.
- 11.Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Automat. Control, 2004, 49: 1520−1533.
- 12.Ren, W.; Beard, R.W.; Atkins, E.M. Information consensus in multivehicle cooperative control. IEEE Control Syst. Mag., 2007, 27: 71−82.
- 13.Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE, 2007, 95: 215−233.
- 14.He, W.L.; Xu, B.; Han, Q.L.; et al. Adaptive consensus control of linear multiagent systems with dynamic event-triggered strategies. IEEE Trans. Cybernet., 2020, 50: 2996−3008.
- 15.Cattivelli, F.S.; Sayed, A.H. Diffusion strategies for distributed Kalman filtering and smoothing. IEEE Trans. Automat. Control, 2010, 55: 2069−2084.
- 16.Hu, J.W.; Xie, L.H.; Zhang, C.S. Diffusion Kalman filtering based on covariance intersection. IEEE Trans. Signal Process., 2012, 60: 891−902.
- 17.Fantacci, C.; Vo, B.N.; Vo, B.T.; et al. Robust fusion for multisensor multiobject tracking. IEEE Signal Process. Lett., 2018, 25: 640−644.
- 18.Uhlmann, J.K. Dynamic Map Building and Localization: New Theoretical Foundations. Ph.D. Thesis, University of Oxford, Oxford, 1995.
- 19.Hurley, M.B. An information theoretic justification for covariance intersection and its generalization. In Proceedings of the 5th International Conference on Information Fusion, Annapolis, 08–11 July 2002; IEEE: Annapolis, 2002; pp. 505–511. doi: 10.1109/ICIF.2002.1021196.
- 20.Taylor, C.N.; Bishop, A.N. Homogeneous functionals and bayesian data fusion with unknown correlation. Information Fusion, 2019, 45: 179−189.
- 21.Bailey, T.; Julier, S.; Agamennoni, G. On conservative fusion of information with unknown non-Gaussian dependence. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 09–12 July 2012; IEEE: Singapore, 2012; pp. 1876–1883. doi: 10.1016/j.inffus.2018.02.002.
- 22.Grime, S.; Durrant-Whyte, H.F. Data fusion in decentralized sensor networks. Control Eng. Pract., 1994, 2: 849−863.
- 23.Makarenko, A.; Brooks, A.; Kaupp, T.; et al. Decentralised data fusion: A graphical model approach. In Proceedings of the 12th International Conference on Information Fusion, Seattle, 06–09 July 2009; IEEE: Seattle, 2009; pp. 545–554.
- 24.Battistelli, G.; Chisci, L. Kullback–Leibler average, consensus on probability densities, and distributed state estimation with guaranteed stability. Automatica, 2014, 50: 707−718.
- 25.Julier, S.J. An empirical study into the use of chernoff information for robust, distributed fusion of gaussian mixture models. In Proceedings of the 2006 9th International Conference on Inf. Fusion, Florence, 10–13 July 2006; IEEE: Florence, 2006. doi: 10.1109/ICIF.2006.301755.
- 26.Li, T.C.; Corchado, J.M.; Sun, S.D. On generalized covariance intersection for distributed PHD filtering and a simple but better alternative. In Proceedings of the 20th International Conference on Information Fusion, Xi'an, 10–13 July 2017; IEEE: Xi'an, 2017. doi: 10.23919/ICIF.2017.8009732.
- 27.Farrell, W.J.; Ganesh, C. Generalized chernoff fusion approximation for practical distributed data fusion. In Proceedings of the 12th International Conference on Information Fusion, Seattle, 06–09 July 2009; IEEE: Seattle, 2009; pp. 555–562.
- 28.Uhlmann, J.K. Covariance consistency methods for fault-tolerant distributed data fusion. Inf. Fusion, 2003, 4: 201−215.
- 29.Friedman, N. Seapower as Strategy: Navies and National Interests; Naval Institute Press: Annapolis, 2001.
- 30.Chang, K.; Chong, C.Y.; Mori, S. Analytical and computational evaluation of scalable distributed fusion algorithms. IEEE Trans. Aerosp. Electron. Syst., 2010, 46: 2022−2034.
- 31.Chong, C.Y.; Mori, S. Convex combination and covariance intersection algorithms in distributed fusion. In Proceedings of the 4th International Conference on Information Fusion, Montreal; Montreal, 2001. Available online:https://www.semanticscholar.org/paper/Convex-Combination-and-Covariance-Intersection-in-Chong/184648882646f20062bf8f4fd0514ccd82253978 (accessed on15 October 2022)
- 32.Welch, G.; Bishop, G. SCAAT: Incremental tracking with incomplete information. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, New York, August 1997; Addison-Wesley Publishing Co: New York, 1997; pp. 333–344. doi: 10.1145/258734.258876.
- 33.Zhu, H.Y.; Zhai, Q.Z.; Yu, M.W.; et al. Estimation fusion algorithms in the presence of partially known cross-correlation of local estimation errors. Inf. Fusion, 2014, 18: 187−196.
- 34.Battistelli, G.; Chisci, L.; Mugnai, G.; et al. Consensus-based linear and nonlinear filtering. IEEE Trans. Automat. Control, 2015, 60: 1410−1415.
- 35.Julier, S.J.; Uhlmann, J.K. Using covariance intersection for SLAM. Robot. Auton. Syst., 2007, 55: 3−20.
- 36.Niehsen, W. Information fusion based on fast covariance intersection filtering. In Proceedings of the 5th International Conference on Information Fusion, Annapolis, 08–11 July 2002; IEEE: Annapolis, 2002; pp. 901–904. doi: 10.1109/ICIF.2002.1020907.
- 37.Clarke, D. Minimum information loss fusion in distributed sensor networks. In 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, 05–08 July 2016; IEEE: Heidelberg, 2016; pp. 1057–1062.
- 38.Mahler, R.P.S. Optimal/robust distributed data fusion: A unified approach. In Proceedings of SPIE 4052, Signal Processing, Sensor Fusion, and Target Recognition IX, Orlando, 4 August 2000; SPIE: Orlando, 2000. doi: 10.1117/12.395064.
- 39.Wang, Y.M.; Li, X.R. Distributed estimation fusion under unknown cross-correlation: An analytic center approach. In Proceedings of the 2010 14th International Conference on Information Fusion, Edinburgh, 26–29 July 2010; IEEE: Edinburgh, 2010. doi: 10.1109/ICIF.2010.5711989.
- 40.Wu, T.T.; An, J.; Ding, C.S.; Luo, S.X. Research on ellipsoidal intersection fusion method with unknown correlation. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 09–12 July 2012; IEEE: Singapore, 2012; pp. 558–564.
- 41.Deng, Z.L.; Zhang, P.; Qi, W.J.; et al. Sequential covariance intersection fusion Kalman filter. Inf. Sci., 2012, 189: 293−309.
- 42.Ajgl, J.; Straka, O. A geometrical perspective on fusion under unknown correlations based on Minkowski sums. In Proceedings of the 2017 20th International Conference on Information Fusion, Xi'an, 10–13 July 2017; IEEE: Xi'an, 2017. doi: 10.23919/ICIF.2017.8009722.
- 43.Ajgl, J.; Straka, O. Covariance intersection in track-to-track Fusion: Comparison of fusion configurations. IEEE Trans. Ind. Inf., 2018, 14: 1127−1136.
- 44.Deng, Z.L.; Zhang, P.; Qi, W.J.; et al. The accuracy comparison of multisensor covariance intersection fuser and three weighting fusers. Inf. Fusion, 2013, 14: 177−185.
- 45.Üney, M.; Clark, D.E.; Julier, S.J. Distributed fusion of PHD filters via exponential mixture densities. IEEE J. Sel. Top. Signal Process., 2013, 7: 521−531.
- 46.Ahmed, N.R.; Campbell, M. Fast consistent Chernoff fusion of Gaussian mixtures for ad hoc sensor networks. IEEE Trans. Signal Process., 2012, 60: 6739−6745.
- 47.Gunay, M.; Orguner, U.; Demirekler, M. Chernoff fusion of Gaussian mixtures based on sigma-point approximation. IEEE Trans. Aerosp. Electron. Syst., 2016, 52: 2732−2746.
- 48.Benaskeur, A.R. Consistent fusion of correlated data sources. In Proceedings of 28th Annual Conference of the Industrial Electronics Society, Seville, 05–08 November 2002; IEEE: Seville, 2002; pp. 2652–2656. doi: 10.1109/IECON.2002.1182812.
- 49.Zhou, Y.; Li, J.X. Data fusion of unknown correlations using internal ellipsoidal approximation. IFAC Proc. Vol., 2008, 41: 2856−2860.
- 50.Vazhentsev, A.Y. On internal ellipsoidal approximations for problems of control synthesis with bounded coordinates. J. Computer Syst. Sci. Int., 2000, 39: 399−406.
- 51.Sijs, J.; Lazar, M. State fusion with unknown correlation: Ellipsoidal intersection. Automatica, 2012, 48: 1874−1878.
- 52.Ajgl, J.; Straka, O. On weak points of the ellipsoidal intersection fusion. In Proceedings of 2017 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Daegu, 16–18 November 2017; IEEE: Daegu, 2017. doi: 10.1109/MFI.2017.8170403.
- 53.Noack, B.; Sijs, J.; Reinhardt, M.; et al. Decentralized data fusion with inverse covariance intersection. Automatica, 2017, 79: 35−41.
- 54.Noack, B.; Sijs, J.; Hanebeck, U.D. Inverse covariance intersection: New insights and properties. In Proceedings of the 20th International Conference on Information Fusion, Xi'an, 10–13 July 2017; IEEE: Xi'an, 2017. doi: 10.23919/ICIF.2017.8009694.
- 55.Yang, F.W.; Li, Y.M. Set-membership filtering for systems with sensor saturation. Automatica, 2009, 45: 1896−1902.
- 56.Bakr, M.A.; Lee, S. Track level fusion with an estimation of maximum bound of unknown correlation. In Proceedings of 2016 International Conference on Control, Automation and Information Sciences (ICCAIS), Ansan, 27–29 October 2016; IEEE: Ansan, 2016. doi: 10.1109/ICCAIS.2016.7822431.
- 57.Leonardos, S.; Daniilidis, K. A game-theoretic approach to robust fusion and kalman filtering under unknown correlations. In Proceedings of the 36th American Control Conference, Seattle, 24–26 May 2017; IEEE: Seattle, 2017. doi: 10.23919/ACC.2017.7963339.
- 58.Zhang, X.H. An optimal data fusion algorithm in the presence of unknown cross covariances. IEEE Trans. Automat. Control, 2020, 65: 1226−1233.
- 59.Shirsat, A.; Mishra, S.; Zhang, W.L.; et al. Probabilistic consensus on feature distribution for multi-robot systems with Markovian exploration dynamics. IEEE Robot. Autom. Lett., 2022, 7: 6407−6414.
- 60.Li, W.L.; Jia, Y.M. Distributed estimation for Markov jump systems via diffusion strategies. IEEE Trans. Aerosp. Electron. Syst., 2017, 53: 448−460.
- 61.Franken, D.; Hupper, A. Improved fast covariance intersection for distributed data fusion. In Proceedings of the 7th International Conference on Information Fusion, Philadelphia, 25–28 July 2005; IEEE: Philadelphia, 2005. doi: 10.1109/ICIF.2005.1591849.
- 62.Cong, J.L.; Li, Y.Y.; Qi, G.Q.; et al. An order insensitive sequential fast covariance intersection fusion algorithm. Inf. Sci. 2016, 367–368, 28–40. doi: 10.1016/j.ins.2016.06.001.
- 63.Reinhardt, M.; Noack, B.; Hanebeck, U.D. Closed-form optimization of covariance intersection for low-dimensional matrices. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 09–12 July 2012; IEEE: Singapore, 2012; pp. 1891–1896.
- 64.Xiao, L.; Boyd, S.; Lall, S. A scheme for robust distributed sensor fusion based on average consensus. In Proceedings of 4th International Symposium on Information Processing in Sensor Networks, Boise, 15 April 2005; IEEE: Boise, 2005; pp. 63–70. doi: 10.1109/IPSN.2005.1440896.
- 65.Li, W.Y.; Wei, G.L.; Han, F.; et al. Weighted average consensus-based unscented Kalman filtering. IEEE Trans. Cybernet., 2016, 46: 558−567.
- 66.Battistelli, G.; Chisci, L.; Fantacci, C. Parallel consensus on likelihoods and priors for networked nonlinear filtering. IEEE Signal Process. Lett., 2014, 21: 787−791.
- 67.Battistelli, G.; Chisci, L. Stability of consensus extended Kalman filter for distributed state estimation. Automatica, 2016, 68: 169−178.
- 68.Liu, Q.Y; Wang, Z.D.; He, X.; et al. On Kalman-consensus filtering with random link failures over sensor networks. IEEE Trans. Automat. Control, 2018, 63: 2701−2708.
- 69.Wang, B.L.; Yi, W.; Hoseinnezhad, R.; et al. Distributed fusion with multi-bernoulli filter based on generalized covariance intersection. IEEE Trans. Signal Process., 2017, 65: 242−255.
- 70.Li, W.Y.; Wang, Z.D.; Ho, D.W.C.; et al. On boundedness of error covariances for Kalman consensus filtering problems. IEEE Trans. Automat. Control, 2020, 65: 2654−2661.
- 71.Li, W.Y.; Yang, F.W.; Wei, G.L. A novel observability gramian-based fast covariance intersection rule. IEEE Signal Process. Lett., 2018, 25: 1570−1574.
- 72.Julier, S.J.; Uhlmann, J.K. General decentralized data fusion with covariance intersection (CI). In Handbook of Data Fusion. CRC Press, 2001. Available online:https://www.taylorfrancis.com/chapters/edit/10.1201/9781420053098-19/general-decentralized-data-fusion-covariance-intersection-simon-julier-jeffrey-uhlmann (accessed on 14 October 2022)
- 73.Hanebeck, U.D.; Briechle, K.; Horn, J. A tight bound for the joint covariance of two random vectors with unknown but constrained cross-correlation. In Proceedings of the Conference Documentation International Conference on Multisensor Fusion and Integration for Intelligent Systems, Baden-Baden, 20–22 August 2001; IEEE: Baden-Baden, 2001. doi: 10.1109/MFI.2001.1013513.
- 74.Reece, S.; Roberts, S. Robust, low-bandwidth, multi-vehicle mapping. In Proceedings of the 2005 7th International Conference on Information Fusion, Philadelphia, 25–28 July 2005; IEEE: Philadelphia, 2005. doi: 10.1109/ICIF.2005.1592009.
- 75.Boyd, S.; El Ghaoui, L.; Feron, E.; et al. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, 1994; p. 15.
- 76.Kaplan, L.M.; Blair, W.D.; Bar-Shalom, Y. Simulations studies of multisensor track association and fusion methods. In Proceedings of 2006 IEEE Aerospace Conference, Big Sky, 04–11 March 2006; IEEE: Big Sky. doi: 10.1109/AERO.2006.1655913.
- 77.Qu, X.M.; Zhou, J.; Song, E.B.; Zhu, Y.M. Minimax robust optimal estimation fusion in distributed multisensor systems with uncertainties. IEEE Signal Process. Lett., 2010, 17: 811−814.
- 78.Ajgl, J.; Straka, O. Rectification of partitioned covariance intersection. In Proceedings of the 38th American Control Conference, Philadelphia, 10–12 July 2019; IEEE: Philadelphia, 2019; pp. 5786–5791. doi: 10.23919/ACC.2019.8814466.
- 79.Petersen, A.; Beyer, M.A. Partitioned covariance intersection. In Proceedings of International Symposium Information on Ships, 2001. Available online:https://scholar.google.co.jp/scholar?hl=en&as_sdt=0%2C5&as_vis=1&q=Partitioned+covariance+intersection&btnG= (accessed on 16 October 2022)
- 80.Chen, B.; Hu, G.Q.; Ho, D.W.C.; et al. Distributed covariance intersection fusion estimation for cyber-physical systems with communication constraints. IEEE Trans. Automat. Control, 2016, 61: 4020−4026.
- 81.Battistelli, G.; Chisci, L.; Selvi, D. A distributed kalman filter with event-triggered communication and guaranteed stability. Automatica, 2018, 93: 75−82.
- 82.Chang, T.K.; Mehta, A. Control-theoretical and topological analysis of covariance intersection based distributed Kalman filter. IEEE Control Syst. Lett., 2018, 2: 665−670.
- 83.Wang, S.C.; Ren, W. On the convergence of distributed estimation of LTV dynamic system with switching directed topologies and time-varying sensing models. In Proceedings of the 2016 35th American Control Conference, Boston, 06–08 July 2016; IEEE: Boston, 2016. doi: 10.1109/ACC.2016.7526522.
- 84.Wang, S.C.; Ren, W. On the consistency and confidence of distributed dynamic state estimation in wireless sensor networks. In Proceedings of 54th IEEE Conference on Decision and Control (CDC), Osaka, 15–18 December 2015; IEEE: Osaka, 2015; pp. 3069–3074. doi: 10.1109/CDC.2015.7402680.
- 85.Wang, S.C.; Ren, W. On the convergence conditions of distributed dynamic state estimation using sensor networks: A unified framework. IEEE Trans. Control Syst. Technol., 2018, 26: 1300−1316.
- 86.He, X.K.; Xue, W.C.; Fang, H.T. Consistent distributed state estimation with global observability over sensor network. Automatica, 2018, 92: 162−172.
- 87.Olfati-Saber, R. Distributed Kalman filtering for sensor networks. In Proceedings of 46th IEEE Conference on Decision and Control, New Orleans, 12–14 December 2007; IEEE: New Orleans, 2007; pp. 5492–5498. doi: 10.1109/CDC.2007.4434303.
- 88.Wei, G.L.; Li, W.Y.; Ding, D.R.; Liu, Y.R. Stability analysis of covariance intersection-based Kalman consensus filtering for time-varying systems. IEEE Trans. Syst. Man Cybernet. Syst., 2020, 50: 4611−4622.
- 89.Battistelli, G.; Chisci, L.; Morrocchi, S.; et al. An information-theoretic approach to distributed state estimation. IFAC Proc. Vol., 2011, 44: 12477−12482.
- 90.Olfati-Saber, R.; Shamma, J.S. Consensus filters for sensor networks and distributed sensor fusion. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, 15 December 2005; IEEE: Seville, 2005; pp. 6698–6703. doi: 10.1109/CDC.2005.1583238.
- 91.Olfati-Saber, R. Distributed Kalman filter with embedded consensus filters. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, 15 December 2005; IEEE: Seville, 2005; pp. 8179–8184. doi: 10.1109/CDC.2005.1583486.
- 92.Olfati-Saber, R. Kalman-consensus filter: Optimality, stability, and performance. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, 15–18 December 2009; IEEE: Shanghai, 2009. doi: 10.1109/CDC.2009.5399678.
- 93.Shen, B.; Wang, Z.D.; Hung, Y.S. Distributed H∞-consensus filtering in sensor networks with multiple missing measurements: The finite-horizon case. Automatica, 2010, 46: 1682−1688.
- 94.Ugrinovskii, V. Distributed robust filtering with H∞ consensus of estimates. Automatica, 2011, 47: 1−13.
- 95.Han, F.; Wei, G.L.; Ding, D.R.; et al. Local condition based consensus filtering with stochastic nonlinearities and multiple missing measurements. IEEE Trans. Automat. Control, 2017, 62: 4784−4790.
- 96.Kamgarpour, M.; Tomlin, C. Convergence properties of a decentralized Kalman filter. In Proceedings of 2008 47th IEEE Conference on Decision and Control, Cancun, 09–11 December 2008; IEEE: Cancun, 2008; pp. 3205–3210. doi: 10.1109/CDC.2008.4738989.
- 97.Li, W.Y.; Wei, G.L.; Ho, D.W.C.; et al. A weightedly uniform detectability for sensor networks. IEEE Trans. Neural Networks Learn. Syst., 2018, 29: 5790−5796.
- 98.Battistelli, G.; Chisci, L.; Fantacci, C.; et al. Consensus-based multiple-model Bayesian filtering for distributed tracking. IET Radar Sonar Navigat., 2014, 9: 401−410.
- 99.Yang, H.J.; Li, H.; Xia, Y. Q; et al. Distributed kalman filtering over sensor networks with transmission delays. IEEE Trans. Cybernet., 2021, 51: 5511−5521.
- 100.Lopes, C.G.; Sayed, A.H. Diffusion least-mean squares over adaptive networks: Formulation and performance analysis. IEEE Trans. Signal Process., 2008, 56: 3122−3136.
- 101.Tu, S.Y.; Sayed, A.H. Diffusion strategies outperform consensus strategies for distributed estimation over adaptive networks. IEEE Trans. Signal Process., 2012, 60: 6217−6234.
- 102.Uney, M.; Clark, D.E.; Julier, S.J. Information measures in distributed multitarget tracking. In Proceedings of the 14th International Conference on Information Fusion, Chicago, 5–8 July 2011; IEEE: Chicago, 2011.
- 103.Clark, D.; Julier, S.; Mahler, R.; et al. Robust multi-object sensor fusion with unknown correlations. In Proceedings of the Sensor Signal Processing for Defence (SSPD 2010), London, 29–30 September 2010; IET: London, 2010. doi: 10.1049/ic.2010.0233.
- 104.Battistelli, G.; Chisci, L.; Fantacci, C.; et al. Consensus CPHD filter for distributed multitarget tracking. IEEE J. Sel. Top. Signal Process., 2013, 7: 508−520.
- 105.Vo, B.T.; Vo, B.N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process., 2013, 61: 3460−3475.
- 106.Li, H.; Nashashibi, F.; Yang, M. Split covariance intersection filter: Theory and its application to vehicle localization. IEEE Trans. Intellig. Transp. Syst., 2013, 14: 1860−1871.
- 107.Lazarus, S.B.; Ashokaraj, I.; Tsourdos, A.; et al. Vehicle localization using sensors data fusion via integration of covariance intersection and interval analysis. IEEE Sensors J., 2007, 7: 1302−1314.
- 108.Guo, Q.; Chen, S.Y.; Leung, H.; et al. Covariance intersection based image fusion technique with application to pansharpening in remote sensing. Inf. Sci., 2010, 180: 3434−3443.
- 109.Shi, Y.; Yang, X.Y.; Cheng, T. Pansharpening of multispectral images using the nonseparable framelet lifting transform with high vanishing moments. Inf. Fusion, 2014, 20: 213−224.
- 110.Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Automat. Mag., 2006, 13: 99−110.
- 111.Ritter, T.; Euler, J.; Ulbrich, S.; et al. Decentralized dynamic data-driven monitoring of atmospheric dispersion processes. Proc. Computer Sci., 2016, 80: 919−930.
- 112.Bar-Shalom, Y. On the track-to-track correlation problem. IEEE Trans. Automat. Control, 1981, 26: 571−572.
- 113.Yang, F.W.; Wang, Z.D.; Hung, Y.S. Robust Kalman filtering for discrete time-varying uncertain systems with multiplicative noises. IEEE Trans. Automat. Control, 2002, 47: 1179−1183.
- 114.Dong, Z.; You, Z. Finite-horizon robust kalman filtering for uncertain discrete time-varying systems with uncertain-covariance white noises. IEEE Signal Process. Lett., 2006, 13: 493−496.
- 115.Wang, Y.L.; Djurić, P.M. Distributed Bayesian estimation of linear models with unknown observation covariances. IEEE Trans. Signal Process., 2016, 64: 1962−1971.
- 116.Zhou, K.M.; Doyle, J.C.; Glover, K. Robust and Optimal Control; Prentice Hall: Upper Saddle River, 1995.
- 117.Hu, J.; Wang, Z.D.; Gao, H.J.; et al. Extended kalman filtering with stochastic nonlinearities and multiple missing measurements. Automatica, 2012, 48: 2007−2015.
- 118.Yang, G.H.; Wang, J.L. Robust nonfragile Kalman filtering for uncertain linear systems with estimator gain uncertainty. IEEE Trans. Automat. Control, 2001, 46: 343−348.
- 119.Doyle, J.; Glover, K.; Khargonekar, P.; et al. State-space solutions to standard H2 and H∞ control problems. IEEE Trans. Automat. Control, 1989, 34: 831−847.
- 120.Raich, A.; Çinar, A. Diagnosis of process disturbances by statistical distance and angle measures. Comput. Chem. Eng., 1997, 21: 661−673.
- 121.Li, W.Y.; Yang, F.W.; Thiel, D.V.; et al. Minimal number of sensor nodes for distributed kalman filtering. IEEE Trans. Syst. Man Cybernet. Syst., 2022, 52: 1778−1786.
- 122.Deyst, J.; Price, C. Conditions for asymptotic stability of the discrete minimum-variance linear estimator. IEEE Trans. Automat. Control, 1968, 13: 702−705.
- 123.Li, W.Y.; Wei, G.L.; Ding, D.R.; et al. A new look at boundedness of error covariance of Kalman filtering. IEEE Trans. Syst. Man Cybernet. Syst., 2018, 48: 309−314.
- 124.Anderson, B.D.O.; Moore, J.B. Detectability and stabilizability of time-varying discrete-time linear systems. SIAM J. Control Optimizat., 1981, 19: 20−32.
- 125.Li, W.Y.; Wei, G.L.; Yang, F.W. Uniform detectability-aided boundedness analysis of error covariances of kalman filter for time-varying systems. IEEE Trans. Syst. Man Cybernet. Syst., 2022, 52: 4798−4806.
How to Cite
Wangyan Li; Fuwen Yang. Information Fusion over Network Dynamics with Unknown Correlations: An Overview. International Journal of Network Dynamics and Intelligence 2023, 2 (2), 100003. https://doi.org/10.53941/ijndi0201003.
RIS
BibTex
Copyright & License

Copyright (c) 2023 by the authors.
This work is licensed under a Creative Commons Attribution 4.0 International License.
Contents
References


