The principal purpose of this work was to study the spread of brucellosis in the state of São Paulo with the help of the complex network theory and to propose control measures for its eradication. For this, the scale-free model of complex networks, widely known in the literature, was used. The effect of vaccination was verified in each of the municipalities in the state of São Paulo and it was observed that when heterogeneity is not taken into account, vaccination becomes ineffective for the eradication of the disease.
- Open Access
- Article
Individual-Based Modelling of Animal Brucellosis Spread with the Use of Complex Networks
- E.R. Pinto 1,
- E.G. Nepomuceno 2, *,
- A.S.L.O. Campanharo 1
Author Information
Received: 12 Oct 2022 | Accepted: 23 Nov 2022 | Published: 22 Dec 2022
Abstract
Graphical Abstract
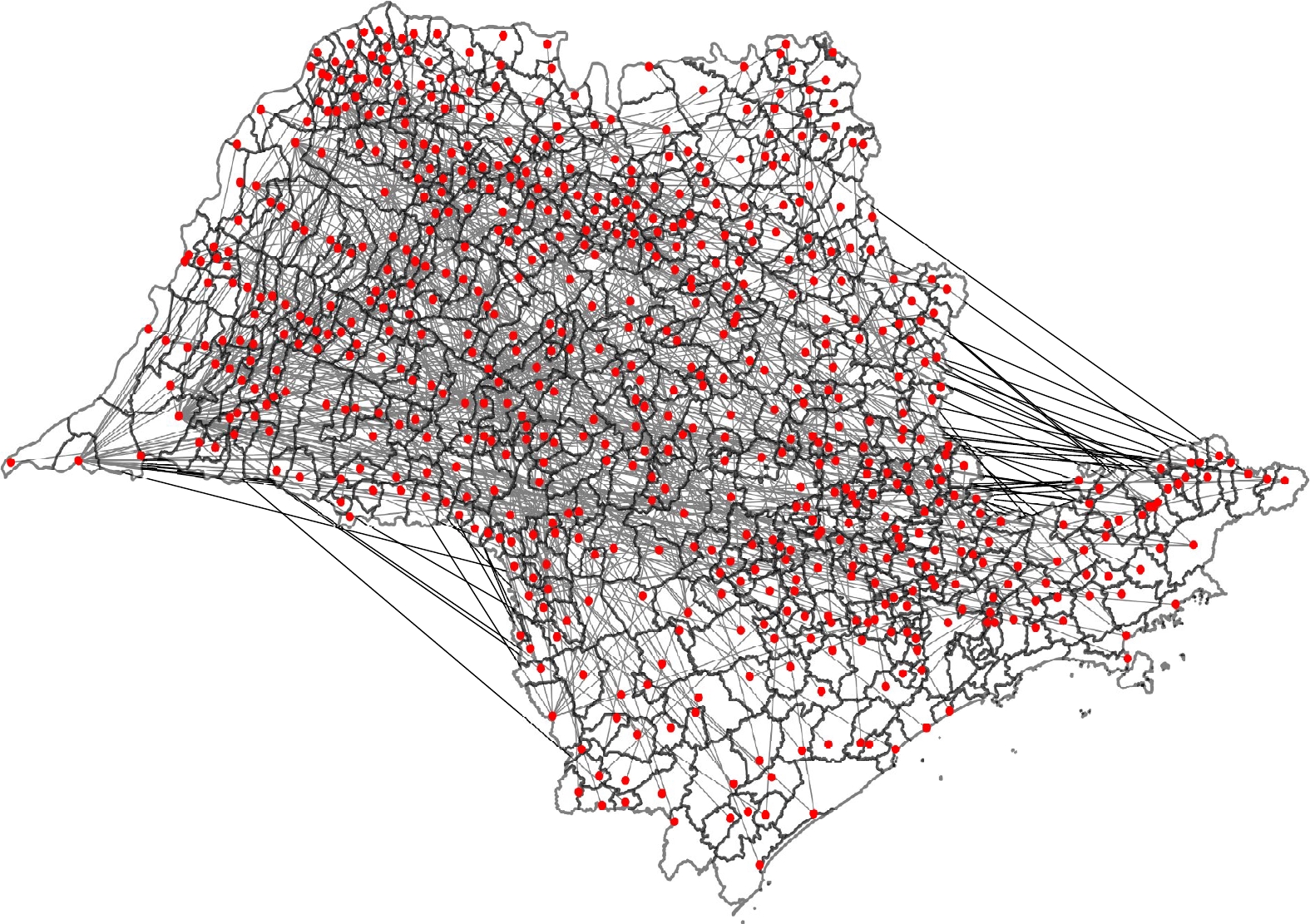
Keywords
References
- 1.Paulin, L.M.; Ferreira Neto, J. S, A experiência Brasileira no combate à Brucelose bovina. Arq. Inst. Biol., 2002, 69: 105−112.
- 2.Pappas, G.; Papadimitriou, P.; Akritidis, N.;, et al, The new global map of human brucellosis. Lancet Infect. Dis., 2006, 6: 91−99.
- 3.Franc, K.A.; Krecek, R.C.; Häsler, B.N.;, et al, Brucellosis remains a neglected disease in the developing world: A call for interdisciplinary action. BMC Public Health, 2018, 18: 125.
- 4.de Souza, V.A.F.; Ferreira Neto, J.S.; Amaku, M.;, et al, Mathematical modeling of bovine brucellosis control using the RB51 vaccine. Semin. Ciênc. Agrár., 2016, 37: 3767−3776.
- 5.Borba, M.R.; Stevenson, M.A.; Gonçalves, V.S.P.;, et al, Prevalence and risk-mapping of bovine brucellosis in Maranhão state, Brazil. Prev. Vet. Med., 2013, 110: 169−176.
- 6.Inchaisri, C.; Prasomsri, P.; Boonserm, T.;, et al, A stochastic simulation model for brucellosis eradication in goat flocks in an area with high flock prevalence but low animal prevalence. Small Rumin. Res., 2016, 136: 227−237.
- 7.H ou, Q.; Zhang, F, Global dynamics of a general brucellosis model with discrete delay. J. Appl. Anal. Comput., 2016, 6: 227−241.
- 8.de Alencar Mota, A.L.A.; Ferreira, F.; Ferreira Neto, J.S.;, et al, Large-scale study of herd-level risk factors for bovine brucellosis in Brazil. Acta Trop., 2016, 164: 226−232.
- 9.Abatih, E.; Ron, L.; Speybroeck, N.;, et al, Mathematical analysis of the transmission dynamics of brucellosis among bison. Math. Methods Appl. Sci., 2015, 38: 3818−3832.
- 10.L i, M.T.; Pei, X.; Zhang, J.;, et al, Asymptotic analysis of endemic equilibrium to a brucellosis model. Math. Biosci. Eng., 2019, 16: 5836−5850.
- 11.Havas, K.A.; Boone, R.B.; Hill, A.E.;, et al, A brucellosis disease control strategy for the kakheti region of the country of Georgia: An agent-based model. Zoonoses Public Health, 2014, 61: 260−270.
- 12.Nepomuceno, E.G.; Barbosa, A.M.; Silva, M.X.;, et al, Individual-based modelling and control of bovine brucellosis. R. Soc. Open Sci., 2018, 5: 180200.
- 13.R oy, S.; McElwain, T.F.; Wan, Y, A network control theory approach to modeling and optimal control of zoonoses: Case study of brucellosis transmission in Sub-Saharan Africa. PLoS Negl. Trop. Dis., 2011, 5: e1259.
- 14.Cipullo, R.I.; Grisi-Filho, J.H.H.; Dias, R.A.;, et al, Cattle movement network, herd size, and bovine brucellosis in the state of Mato Grosso, Brazil. Semin. Ciênc. Agrár., 2016, 37: 3777−3792.
- 15.Darbon, A.; Valdano, E.; Poletto, C.;, et al, Network-based assessment of the vulnerability of Italian regions to bovine brucellosis. Prev. Vet. Med., 2018, 158: 25−34.
- 16.Amaku, M.; Dias, R.A.; Ferreira Neto, J.S.;, et al, Modelagem matemática do controle de Brucelose bovina por vacinação. Arq. Bras. Med. Vet. Zootec., 2009, 61: 135−141.
- 17.Lentz, H.H.K.; Koher, A.; Hövel, P.;, et al, Disease spread through animal movements: A static and temporal network analysis of pig trade in Germany. PLoS One, 2016, 11: e0155196.
- 18.Wa ng, Z.; Moreno, Y.; Boccaletti, S.;, et al, Vaccination and epidemics in networked populations—an introduction. Chaos Solitons Fractals, 2017, 103: 177−183.
- 19.Jin, Z.; Li, S.P.; Zhang, X.G.; et al. Epidemiological modeling on complex networks. In
Complex Systems and Networks ; Lü, J.H.; Yu, X.H.; Chen, G.R.; et al., Eds.; Springer: Berlin/Heidelberg, 2016; pp. 51–77. doi: 10.1007/978-3-662-47824-0_3 - 20.Biegus, T.; Kwasnicka, H. Complex networks in the epidemic modelling. In
9th Asian Conference on Intelligent Information and Database Systems ,Kanazawa ,Japan ,April 3–5 ,2017 ; Springer: Kanazawa, Japan, 2017; pp. 202–213. doi: 10.1007/978-3-319-54472-4_20 - 21.Campanharo, A.S.L.O.; Ramos, F. M, Hurst exponent estimation of self-affine time series using quantile graphs. Phys. A, 2016, 444: 43−48.
- 22.Liljeros, F.; Edling, C.R.; Amaral, L.A.N.;, et al, The web of human sexual contacts. Nature, 2001, 411: 907−908.
- 23.Kupennan, M.; Abramson, G. Small world effect in an epidemiological model. In
The Structure and Dynamics of Networks ; Newman, M.; Barabási, A.L.; Watts, D.J., Eds.; Princeton University Press: Princeton, 2011; pp. 489–492. doi: 10.1515/9781400841356.489 - 24.Ch en, S.; White, B.J.; Sanderson, M.W.;, et al, Highly dynamic animal contact network and implications on disease transmission. Sci. Rep., 2014, 4: 4472.
- 25.Ruget, A.S.; Rossi, G.; Pepler, P.T.;, et al, Multi-species temporal network of livestock movements for disease spread. Appl. Netw. Sci., 2021, 6: 15.
- 26.Chaters, G.L.; Johnson, P.C.D.; Cleaveland, S.;, et al, Analysing livestock network data for infectious disease control: An argument for routine data collection in emerging economies. Philos. Trans. R. Soc. B Biol. Sci., 2019, 374: 2180264.
- 27.Nepomuceno, E.G.; Peixoto, M.L.C.; Lacerda, M.J.;, et al, Application of optimal control of infectious diseases in a model-free scenario. SN Comput. Sci., 2021, 2: 405.
- 28.Newman, M.E.J.
Networks: An Introduction . Oxford University Press: New York, 2010. doi: 10.1093/acprof:oso/9780199206650.001.0001 - 29.da F Costa, L.; Rodrigues, F.A.; Travieso, G.;, et al, Characterization of complex networks: A survey of measurements. Adv. Phys., 2007, 56: 167−242.
- 30.Pinto, E.R.; Nepomuceno, E.G.; Campanharo, A.S.L.O, Impact of network topology on the spread of infectious diseases. Trends Comput. Appl. Math., 2020, 21: 95−115.
- 31.Barabási, A.L.; Albert, R, Emergence of scaling in random networks. Science, 1999, 286: 509−512.
- 32.Bakhtiar, T, Optimal intervention strategies for cholera outbreak by education and chlorination. IOP Conf. Ser.: Earth Environ. Sci., 2016, 31: 012022.
- 33.Instituto Brasileiro de Geografia e Estatística.
Censo Agropecuário 2017: Resultados Definitivos ; IBGE: Rio de Janeiro, 2019. Available online: https://loja.ibge.gov.br/censo-agropecuario-2017-resultados-definitivos.html(accessed on 5 November 2022). - 34.Bigras-Poulin, M.; Thompson, R.A.; Chriel, M.;, et al, Network analysis of Danish cattle industry trade patterns as an evaluation of risk potential for disease spread. Prev. Vet. Med., 2006, 76: 11−39.
How to Cite
Pinto, E. R.; Nepomuceno, E. G.; Campanharo, A. S. L. O. Individual-Based Modelling of Animal Brucellosis Spread with the Use of Complex Networks. International Journal of Network Dynamics and Intelligence 2022, 1 (1), 120–129. https://doi.org/10.53941/ijndi0101011.
RIS
BibTex
Copyright & License

Copyright (c) 2022 by the authors.
This work is licensed under a Creative Commons Attribution 4.0 International License.
Contents
References


