Downloads

https://doi.org/10.53941/ijndi0201003
Wangyan Li, & Fuwen Yang. Information Fusion over Network Dynamics with Unknown Correlations: An Overview. International Journal of Network Dynamics and Intelligence. 2023, 2(2), 100003. doi: https://doi.org/10.53941/ijndi0201003
Volume 2, Issue 2, Jun 2023
Copyright (c) 2023 by the authors.
Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

Survey/review study

Information Fusion over Network Dynamics with Unknown Correlations: An Overview

Wangyan Li 1, and Fuwen Yang 2,*

1 College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China

2 Griffth School of Engineering, Griffth University, Gold Coast Campus, QLD 4222, Australia

* Correspondence: fuwen.yang@griffth.edu.au

 

 

Received: 24 October 2022

Accepted: 22 November 2022

Published: 23 June 2023

 

Abstract: Unknown correlations (UCs) generally exist in a wide spectrum of practical multi-source information fusion problems, and thereby, their corresponding fusion problems have become one of the most important topics in information fusion domain. During the past three decades, the research on this topic has been growing rapidly and extensively, and, as a result, various important advances have been reported. In this overview, we intend to summarize the culmination of years of development in the field of information fusion under UCs as a roadmap. First, the potential reasons leading to UCs are investigated. According to the unknown nature of correlations, we further divide UCs into two categories, i.e., fully UCs, and partially UCs. For each category, the corresponding fusion methods are reviewed. Next, this roadmap witnesses the recent development of information fusion under UCs in a distributed way thanks to the popularity of distributed sensing technology. In particular, the distributed fusion techniques based on consensus, diffusion, and multi-object tracking strategies for UCs are examined. Finally, some future perspectives on information fusion under UCs are pointed out.

Keywords:

unknown correlations partially unknown correlations multi-sensor fusion diffusion consensus covariance intersection

1. Introduction

As it is put forward in [1], the essence of information fusion techniques is to combine data from multiple sensors, and related information from associated databases, to achieve improved accuracies and more specific inferences than that could be achieved by the use of a single sensor alone. From a mathematical perspective, the essence of the unbiased linear combination of multiple estimates (let me assume that there are two estimates for the sake of convenience in the following discussion) in a Kalman filter framework is to find gains , such that the fused estimate  is optimized according to a cost function of the fused error covariance  [2,3], i.e.,

where

If the cross-covariances  and  are known, the solution to Equation (1) is the famous Bar Shalom-Campo (BC) fusion equation [4]. Unfortunately, in many practical scenarios, due to a variety of reasons, their cross-covariances are usually unknown, and this phenomenon is often referred to as unknown correlations (UCs) [5], or unavailable cross-correlations [6], or unknown cross-covariances [7].

It should be noticed that, if UCs are not accommodated appropriately, they may degrade system performance significantly. Therefore, there is no wonder that the topic information fusion under UCs has been drawing considerable attention from both theoretic development and industrial applications. Among them, it is the covariance intersection (CI) [5] and its variants that dominate the research in this matter. Generally, these developments are mainly about: (1) improving CI in terms of both efficiency and accuracy, and (2) applying CI to a diversity of industrial tasks. However, CI is somewhat conservative as it treats UCs as completely unknown. Li et al. [8] proposed that it is more reasonable to further divide UCs into two groups: namely, fully UCs and partially UCs with respect to their unknown nature, and based on that available information about UCs, it is promising to develop more efficient fusion methods, see, e.g. [9,10], for some latest results.

Recent advances have witnessed a growing trend in the distributed fusion related topics mainly due to an increasing popularity of the distributed sensing technology. As a result, the information fusion under UCs in a distributed way has been attracting considerable attention, where distributed strategies such as consensus [11-14], diffusion [15,16], and multi-object tracking [17] have been adopted. In this overview, we provide a roadmap that outlines a series of developments and advances of the information fusion methods under UCs. It follows a roadmap depicted in Figure 1. The remainder of this overview is given as follows. In Section 2, the potential reasons leading to UCs are presented. According to the way that it deals with UCs, the information fusion methods under UCs are grouped into three categories, i.e., fusion under fully UCs, fusion under partially UCs, and distributed fusion under UCs, and they are reviewed in Sections 3−5, respectively. Section 6 concludes this overview with some future perspectives.

Notation. Throughout this review, we adhere to the following notations if not specified otherwise: For a matrix , , and  separately represent its transpose and inverse.  (respectively, ) means matrix  is positive definite (respectively, positive semi-definite).  and  are the shorthands for the trace and determinant of the matrix . Besides,  is the identity matrix with dimension .  is a set of  sensor nodes. An edge  indicates node  can receive information from node . If node  is included in its neighbors, we denote this neighborhood as  ( ); otherwise, we denote it by .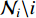

Figure 1. A roadmap of the development of fusion under unknown correlations.

2. Root Causes of Unknown Correlations

Unknown correlations (UCs) [5] are commonly referred to as unavailable cross-correlations [6], or unknown cross-covariances [7]. Based on the literature reviewed, the main reasons attributing to UCs can be grouped into the following two categories:

(1) Lack of knowledge of the true system

• Unidentified correlations — Correlations, as yet unidentified, may occur during the vehicle motion, where the observation noises of a suite of navigation sensors mounted on the same vehicle might be correlated with one another [5].

• Unguaranteed assumptions — It is often widely believed that the errors associated with the current system estimate and the new measurement are uncorrelated; however, this is not true as any nonlinear transformation will equitably introduce time-correlated errors, which may introduce a certain degree of unknown correlations in the final implementation [18]. Another example can be found in robotic control systems where it is common to assume data-flows among multiple interconnected algorithms are independent; however, there is no guarantee of this mutual independence in practice [19]. The other scenario usually arises in probabilistic fusion approaches. When combining information from varied sensors, the corresponding conditional probabilities are usually presumably conditionally independent, however, such an assumption is not genuinely guaranteed [20].

(2) Correlations that are either too expensive to maintain or too difficult to describe

• Difficulties in maintaining — The process models of applications such as weather forecasting, and map-making could involve hundreds of thousands of variables, which suggests that maintaining a complete history of covariances becomes impossible [5]. Another example can be found in the decentralized data fusion within the Bayesian framework, where it requires dependence between uncertain variables to be defined in terms of joint or conditional probability density functions (PDFs). However, maintaining this joint structure will probably incur significant bookkeeping and communications overhead, and impose strong constraints on network topology. Hence, a feasible implementation may necessitate suboptimal fusion procedures that discard some dependency information [ 21].

• Double counting [22,23] or data incest [24] phenomena — Owing to the fact that, instead of the raw sensor data, it is the estimates that propagate through the network, the problem of double counting generally exists in distributed information fusion problems [25]. In particular, this phenomenon becomes more severe in networks with potential "network looping" [17], where the common information can travel in loops [26]. Hence, the information may inadvertently be used several times. In this case, the resulting correlation is cumbersome to identify due to that it is related to several aspects including, but not limited to, the fusion protocol, the network topology (except when it is connected through a tree-shape topology where only one single path exists between any pair of sensors [22]), and the number of communicating iterations [26].

• Rumor propagation [27,59]— For example, in a typical distributed tracking systems for tactical military missions, the scenarios contributing to unknown correlations are threefold. First, tactical systems are often consisting of sensor nodes and processing nodes that are connected over the dynamic and unpredictable mobile ad-hoc networks, wherein the processing nodes produce fused solutions rather than the raw sensor measurements. Hence, eliminating redundant data flows between nodes is virtually impractical in real-time. Next, many legacy systems cannot produce statistically independent updates by (1) modifying tracking data [27,59] because of the common process noise, or (2) providing lineage or pedigree information with each estimate that allows its cross-covariance with other estimates to be determined before fusion with a Kalman filter [28]. Lastly, the tracking data shared between the processing nodes is of a variety of statistics such as Gaussian, non-Gaussian, active, and passive [27,59].

In summary, the reasons leading to UCs are abundant. Moreover, it is generally believed that UCs are ubiquitously existing in a diverse range of information fusion and distributed filtering issues, and neglecting the effect of UCs may lead to grave consequences of the deterioration of fusion performance. Hence, there is a great need to tackle this phenomenon effectively. Fortunately, during the past decades, many important theories and applications have been reported in this area. According to the unknown nature of UCs, the fusion methods can be immediately divided into fusion under fully UCs, and fusion under partially UCs.

3. Fusion under Fully Unknown Correlations

In this section, we focus on the advances of the methods developed in dealing with UCs, in particular, fully UCs. Roughly speaking, these developments have gone through three periods: prior to CI, CI, and posterior to CI. Especially, after the introduction of CI in 1997, new improvements, insights, ideas, and applications are reported subsequently. Hence, it is necessary to further review the posterior to CI period in terms of the following three aspects, that is, more accurate CI, faster CI, and applications.

3.1. Prior to Covariance Intersection

Even though the study of multi-sensor fusion technologies can be dated back as early as the beginning of 1970s [29], the road leading to a satisfied fusion solution to address unknown correlations is not smooth mainly due to the intricate nature of unknowns. One intuitive method is the naive fusion [30], or the simple convex combination (SCC) [31], i.e.,

where  and  are the error covariance and estimate of information source , and  and  are fused ones, respectively. This method has been applied in [32] for a head tracking problem. As can be seen from Equations (3) and (4), the method ignores the inherent correlations directly. In this sense, this method is too optimistic [33], and in general cannot guarantee consistent (A filter is said to be consistent if its estimated error covariance  is an upper limit of the true error covariance, i.e., , where  is an unbiased estimate of  [34].) results [35]. To compensate this kind of over-confidence, a common suboptimal approach is established by increasing the process noise manually. However, this heuristic method calls for considerable certain expertise and undermines the foundation of the Kalman filter framework [36]. Another typical solution of avoiding this over-confidence is to rely on artificially inflating the "fused" covariance. However, this method should be considered on case-by-case basis and not reliable as the degree of inflation may not be accurately quantified [20].

3.2. Covariance Intersection

Fortunately, in 1997, the covariance intersection (CI) fusion rule [5], which was first reported by S. J. Julier and J. K. Uhlmann, provided an effective tool to tackle with UCs. The algorithm is detailed as follows:

with

where fusion weights satisfying . Note that, different criteria such as trace and determinant, or the minimum information loss fusion [37] can be used to find optimized weights. Their generalizations include maximizing the peakiness of the distribution [38], or maximizing the complementary squared Mahalanobis distance between the individual and the targeted estimates [39], or minimizing the Bayesian error/Chernoff information or Shannon entropy [19]. In particular, the cost functions  and  are both convex in terms of CI fusion rule [40, Theorem 2].

Compared with the methods prior to CI in dealing with UCs, the CI fusion has the following benefits [41]. (1) The cumbersome procedure of identification and computing of cross covariances is dismissed; (2) It produces a consistent fused estimate, and thereby a non-divergent fuser is established; (3) The accuracy of the fused estimate surpasses that of local ones; (4) It has robustness against UCs as it yields a common upper limit of the true estimation error covariances, and as pointed in [3], this bound is optimal when it fuses two estimates subject to strictly monotonically increasing cost functions such as trace and determinant. As for the fusion of more than two estimates, its sub-optimality was discussed in [42] along with some geometrical explanations [43]. In terms of the fusion accuracy, a comparison was conducted in [44] between CI and three other optimal fusion rules.

Meanwhile, an information-theoretical interpretation of CI, i.e., Chernoff fusion was reported in [19], and its generalization can be found in [30]. Under this justification, the familiar product form of Bayes rule can be understood as the geometric mean, or exponential mixture [45], or weighted Kullback-Leibler average [17,24]. To derive the optimized parameters of the optimal Chernoff fusion exponent in an efficient way, the Monte Carlo importance sampling and the sigma-point approximation methods have been proposed in [46] and [47], respectively.

3.3. Posterior to Covariance Intersection

Due to its superiority over other alternatives, CI has quickly become the first option of fusion methods in dealing with UCs since its induction in 1997. Since then, CI has stimulated much research attention from a broader community to improve, generalize, and apply this fusion method. Generally, those developments can be summarized into the following categories.

3.3.1. More Accurate Covariance Intersection

On the contrary of SCC, CI is too pessimistic [33] as it always guarantees a consistent bound on the error covariances. In this sense, CI is sub-optimal in comparison with the algorithms that can make use of the information about cross-correlation. As a result, during the past two decades, great efforts have been spent to improve the fusing accuracy of CI. Generally, most of them can be classified into the following six groups.

(1) Largest ellipsoidal algorithm [48]. Different from CI that overestimates the intersection region, a new fusion method, called largest ellipsoidal algorithm (LEA) [48], was designed to slightly underestimate this region. The main idea of LEA is to find the largest ellipsoid encompassed by the intersection region. However, as mentioned in [49], LEA did not give a correct derivation of the estimated fusion, which may lead to grave degradation of its estimation performance.

(2) Internal ellipsoidal approximation. For the purpose of closing gaps in [48,49] approximated the intersection region of the covariance matrices with the aid of an internal ellipsoidal approximation (IEA) [50] method, where an iterative algorithm was employed to determine the largest ellipsoid. However, as commented in [51], the iterative nature of this approach may limit its applicability.

(3) Ellipsoidal intersection [51]. Different from the way in which IEA [49] parameterizes the fused estimates, a novel parametrization method proposed in [51], labeled as Ellipsoidal intersection, was proposed to parameterize the correlations, which was conducted a priori to the fusion. However, as pointed out in [3], a drawback of this method is that the obtained covariances underestimate the actual estimation error for certain cross-covariance matrices, thereby the acquired estimates might not be consistent. Also, the assumption about the common prior estimate seems not to be easily satisfied in reality [52].

(4) Inverse covariance intersection [53,54]. Based on the idea to subtract a bound on the maximum possible common information, a new fusion method, i.e., inverse covariance intersection, was developed in [53]. As it can be seen in [53], such a fusion method constituted an optimal way to treat unknown common information. Noack et al. [54] further showed that same fusion rules can be also applied far beyond unknown common information, for example, the problem of common process noise.

(5) Analytic center covariance intersection [39]. Due to the fact that, the minimization criteria of CI mainly focus on the uncertainty of the estimate, rather than the values of the estimates , thereby, the optimal weight  is independent of the values of , which may lead to certain disadvantages. To improve the accuracy, a set-theoretic criterion [55], was proposed to find the analytic center [39]  (or the Chebyshev center [6]) of the solution set , i.e. (Here,  is the potential function of ,  with the squared Mahalanobis distance .),

where both the uncertainty and value of estimates are taken into consideration [39].

(6) Optimal fusion. In case of fusing two measurements with unknown cross-covariances, [56] proposed an optimal fusion method based on the BC formula when both measurements are scalars or their covariance matrices are diagonal. This requirement on measurements was relaxed in [57] to the vector setting by utilizing a game-theoretic approach. As a result, an optimal estimate was obtained in the minimax sense. Note that, the aforementioned results are only limited to two measurements, which is rather restrictive and of limited applications. Recently, a generic optimal data fusion algorithm, namely, numerical projected subgradient optimal fusion, in terms of minimum mean square error (MSE), was developed in [58, Theorem 8] with the capacity of dealing with general number of measurements with any dimension and handling an arbitrary degree of mixture of known and unknown cross-covariances.

3.3.2. Faster CI

Another significant drawback of the CI-like algorithms is the increasing computational intensity. It should be noticed the optimization (7) is indeed a nonlinear optimization problem with constraints in Euclidean space . As the number of to-be-fused information sources grows, the computation itself quickly becomes intractable [41]. The potential reasons for this fact are, but not limited to: (1) the on-line calculations of the fusion weights involve the real-time posteriors of local measurements, but they are often computationally troublesome [26]; (2) when Shannon entropy measure is adopted for more than two inputs, the resulting computational complexity replies on the nature of the PDFs, which may lead to a computationally demanding multi-dimensional optimization problem that contains many local minima [27,59]. Hence, there have been pressing needs to design fast CI algorithms to circumvent this issue. It is no wonder that a number of results, both on-line and off-line ways, have been reported in this spirit.

(1) On-line fast CI.

(a) Sub-optimal non-iterative algorithm. Instead of the nonlinear optimization (7), [36] conceived a sub-optimal non-iterative method such that the fusion weights can be given directly via Equation (9) without optimization, i.e.,

This measure was further adopted in [16,60] for designing a diffusion Kalman filtering scheme, and [6] for a Kullback-Leibler distance (KLD) perspective, that is,

respectively, where 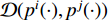 is the KLD from the local probability density functions  to . Later, as compared to Equation (9), a more accurate version was developed in [61] where the weights choosing from

Following the similar paradigm as Equation (11), [27,59] developed a fast Chernoff fusion version of which the weights are chosen by

where ,  and  mean the Shannon Entropies for the Bayesian fusion of all  inputs, the -th input, and all except the -th input, respectively.

(b) Sequential covariance intersection (SCI) [41]. In a sequential manner, [41] transformed the original -dimensional nonlinear optimization problem Equation (7) into  dimensional ones which can be solved effectively via Fibonacci method or gold section method [41]. However, SCI is order sensitive as different fusion results come from different one-dimensional fusion orders. To overcome this disadvantage, an order insensitive SCI fusion algorithm has been developed in [62] with the sub-optimal non-iterative weights Equation (9).

(c) Closed-form optimization [63]. Rather than approximating the optimal weights, [63] gave the exactly optimal weights for the fused covariance matrices of low dimensions with the aid of the proposed closed-form optimization, where the original nonlinear optimization problem was reduced to the polynomial root-finding problem.

(d) Ellipsoidal intersection (EI) [51]. Another exact solution of multi-sensor fusion under unknown correlations is given by EI, where the attained algebraic fusion formulas are computationally accessible.

(2) Off-line fast CI.

Recently, some off-line weights such as Maximum-degree weights and Metropolis weights [64,65] are also used in CI-based distributed filtering schemes such that the computational burden are reduced significantly. The interest applications of this type can be found in [24,34,66-70]. Another type of off-line fast CI was proposed [71], where the fusion weights were calculated via off-line optimization of the observability Gramian.

4. Fusion under Partially Unknown Correlations

With more information about UCs, it is desirable to design better fusion algorithms than the classic CI. Although reasons for UCs may vary, in practice, the following partial information about unknowns can be acquired:

(1) Known independent error components. From the algorithm point of view, CI conservatively assumes that no estimate provides statistically independent information, while the Kalman filter assumes that every estimate provides statistically independent information [72]. Therefore, an ideal data fusion will inevitably involve with some known independent information. In this regard, an extended CI framework called split CI was proposed in [72] to incorporate the known independent error components with consistent fused means and error covariances. In this setting, let  and  with the corresponding error covariances  and , where  and  are correlated to an unknown degree, and  and  are independent of each other completely. It gives the following Split CI equations:

Split CI plays a balance between SCC and CI. If every estimate is statistically independent, it automatically returns to SCC. If there are no statistically independent estimates, it reduces to CI.

(2) Unknown but constrained cross-correlation. If the correlation between the considered random vectors is unconstrained, then a covariance bound exists but with certain conservatism. Less conservative results can be obtained if more information is available. For example, there exists a correlation coefficient bound (one choice of this correlation coefficient bound is given in [10], i.e.,  where  denotes the maximum singular value) such that the maximum absolute of correlation coefficient satisfies . Then a constraint for this cross covariances can be imposed as [73],

Reece and Roberts generalized (14) to include a so-called "centred" matrix , i.e.,

In this regard, [74] developed a bounded covariance inflation fusion approach with the inflated covariance matrix. [9,10] interpreted Equation (14) as a Schur complement condition [75] for positive definiteness, and then the corresponding optimal fusion problems were translated into a Semi-Definite Programming (SDP) problem in terms of minimizing the MSE in the worst case [9], and minimizing the trace of the upper limit of the fused error covariance [10], respectively.

(3) Approximation of unknown covariance. How to exploit correlation coefficients to obtain a cross-covariance matrix without decoupling the degrees of freedom? Kaplan et al. [76] came up an idea to use a single correlation coefficient  to express the cross-covariance of estimation errors from sensors  and  as

where  is the correlation coefficient between two random vectors, and  is the Cholesky decomposition satisfying . In this paradigm, the BC fusion rule [4] can be applied directly by replacing  with  [33].

(4) Norm-bounded uncertainty. Qu et al. [77] explored another way to describe the partial information of unknown correlations where the uncertainty in cross-covariance was formulated in terms of additive norm-bounded terms as follows

where  is the spectral norm or Frobenius norm of matrix,  is the nominal matrix of  and  represents the bound of disturbance in . Then, a linear estimation fusion was developed with the weighting matrix optimized via minimizing the worst-case mean-squared error in the region of uncertainty.

(5) Only one element of cross-correlation matrix is unknown [78]. Suppose  is the cross-covariance matrix of the estimation errors, and all but one individual element of  are known. For this type of the unknown, a partitioned covariance intersection fusion algorithm was designed in [79]. Later, this method was recently improved in [78] where its optimality, and its relation with the fully unknown case were revealed.

5. Distributed Fusion under Unknown Correlations

Recently, a series of developments have been made in the area of distributed sensor networks (DSN) where the unknown correlation is more severe in networks with potential "network looping" [17] phenomenon. As a result, CI has been constantly adopted as a reliable fusion strategy over DSN. However, in a typical DSN, there is no fusion center, and each sensor node only has a limited knowledge from its neighbors. Hence, CI has to be adapted to account for those facts. The following is a general framework of the distributed covariance intersection (DCI) by extending Equations (5) and (6) to the distributed network setting.

Given a distributed sensor network  where  and  are the set of sensor nodes, and connections between them, respectively.  denotes node 's neighborhood that include node . For , it has

with weights  satisfying .

The idea can be traced back to [28] where the purpose of DCI is to provide a fault-tolerant solution to address the inconsistent issues arising from arbitrary, dynamic, distributed network of information processing nodes. Renewed interests of DCI have been focused on its communication constraints, and stability analysis. [80] considered the communication network between the measures and the local fusion center subject to packet dropouts, varying delays, and finite bandwidth; while [81] studied the communication constraint arising from the reduced communication bandwidth in transmitting the local information to its neighbors. Consequently, a novel event-triggered communication strategy was developed. Chang et al. [82] further considered the case that the observation update and the fusion update are based on different topology. Note that all the aforementioned results are accompanied by the corresponding stability analyses, and hence are limited to the time-invariant systems. A time-varying counterpart of stability analysis can be found in [83] which extended the result in [84]. Its generalization has been further discussed in [85] with the consideration of varying communication topology. In terms of the aforementioned stability results, most of them require the system matrix to be nonsingular, and such a requirement is later relaxed in [86].

Based on DCI, with the adoption of consensus and diffusion strategies, the consensus-based CI and diffusion filtering methods are also attracting a significant amount of attention, which will be discussed in details in the following subsections.

5.1. Consensus-Based Covariance Intersection

By combining DCI with the consensus strategy [11,12,87], the consensus-based CI (CCI) is constructed. The general framework of the CCI is given as follows [24,88].

Given a distributed sensor network , for each node , denoting by  and  the information matrix and information vector at time instant  and fusion step  ( ), respectively, with initialization , it has

and weights  satisfying , and  is a given sufficiently small scalar.

The idea of CCI first appeared in [89] for a distributed state estimation problem. Later, a mathematically rigorous treatment of it was given in [24], where CCI is interpreted as a consensus on PDFs in the KLA sense with Metropolis weights. This is also called consensus on information [24,34]. From an algorithm point of view, CCI simply weightedly averages on local information matrices and information vectors in a distributed way. However, compared with the existing consensus filtering methods such as consensus on estimates (The terms consensus on estimates, consensus on measurements, and consensus on information are first coined in [34].) [90-92] (including  consensus filtering [93-95]), and consensus on measurements [34,92,96,97], CCI has the following advantages: (1) only limited few consensus iterations per timestep are needed such that it can reduce the demands of communication resources significantly, (2) it can guarantee the convergence of the filter at any iteration steps [66]; and (3) it can automatically guarantee the consistency of the filter. Following the same consensus philosophy, [98] proposed a consensus-based multiple-model Bayesian filter for distributedly tracking a maneuvering target. This consensus method was later utilized in [34,67] as an indispensable part to design a hybrid consensus filter method. More recently, [68] and [99] investigated the filtering performance of the CCI with the unreliable communication links that are subject to random link failures, and transmission delays, respectively, while [88] studied the consensus properties, detectability, and stability of CCI with the original CI weights in the time-varying system setting.

5.2. Diffusion-Based Covariance Intersection

Differently, by embedding the diffusion strategy [100,101] into DCI, a diffusion-based covariance intersection (DiffCI) fusion can be developed. The strategy of the DiffCI is summarized as follows [16].

Given a distributed sensor network , for each node , it has

where the diffusion matrix  is calculated by

with weights , satisfying .

The diffusion strategy was first proposed in [100]. The main idea is to diffuse information among neighboring nodes via a convex combination so that the estimate at each node is a function of both its temporal data as well as the spatial data across the neighbors [100]. This strategy was applied to [16] a setting of DCI, where the diffusion matrix is obtained based on the fast CI fusion in [36]. Different from the CCI, DiffCI does not require running consensus iterations between information, and is particularly suitable for recursive minimization of cost functions. Recently, [60] extended the DiffCI algorithm to the Markov jump systems.

5.3. Generalized Covariance Intersection-Based Multi-Object Tracking

An emerging area of applications of CI is the multi-object tracking that is a real-time estimation of an unknown yet varying number of objects and their individual trajectories from sensor data [17]. Recent studies have witnessed its development in the distributed settings. However, given that the estimates in different nodes are normally not independent from each other, the practical distributed fusion solution thus falls into suboptimal algorithms such as CI [102]. Following this spirit, Mahler applied the following generalized covariance intersection (GCI) fusion rule [38].

Given two local multi-object posteriors,  and  that are conditioned on measurement set sequences,  and  from two different sensor suites. GCI fuses  and  into an updated multi-object posterior,  by

where  is an integer and .

From the algorithm point of view, GCI is nothing but a mutil-target counterpart of Chernoff fusion. Choices of fusion weights in Equation (22) were explored in [102] based on maximization or minimization of cost measures, or equalizing divergence metrics. Indeed,  in Equation (22) is a real-valued function of a random finite set (RFS) . The evaluation of  is a set integral that integrates over all joint target-spaces, which is computationally prohibitive, thereby the first-order moment statistic is used, i.e., the probability hypothesis density (PHD) is adopted for approximation [103]. The general framework of GCI-based multi-object tracking can be described as follows [104].

Assume that the target set is modelled as an i.i.d. cluster process, the multi-object densities of agent  to be fused take the form

where  is the cardinalized PHD. It is shown GCI fusion yields [103]

where

The algorithms to implement the distributed multi-object tracking can be found in [45]. To save communication and computation in the distributed environment, [26] proposed a more efficient fusion mechanism where, only the significant Gaussian components of local PHD are shared among neighbors and fused. Multi-Bernoulli (MB) filter is another efficient multi-object tracking algorithm as it directly propagates the multi-object distribution instead of its moments [69]. In light of this merit, a distributed multi-object tracking algorithm via using MB filter was proposed in [69]. Note that, the aforementioned results involve multi-object densities with the RFS nature which is difficult to provide the object's unique identity. To alleviate this problem, a labeled RFS was introduced in [105], and [17] proposed analytical expressions for the fusion of labeled MB and marginalized -generalized labeled MB [105, Equation (39)] via KLA.

6. Practical Applications

UCs ubiquitously exist in practice. With the advances of techniques dealing with UCs during the past several decades, a plethora of interesting applications have been reported. In this section, we reviewed these areas where UCs have been successfully dealt with.

(1) Vehicle localization [106,107]. The unknown temporal correlation in absolute positioning measurements (APMs) is dealt with using Split Covariance Intersection Filter (spilt CIF). Specific application examples also illustrate the advantages of spilt CIF and its benefit in vehicle positioning.

(2) Image fusion [108,109]. The image fusion problem can be translated into an estimation problem. With the aid of CI rules, novel image fusion approaches were developed in [108,109] to maintain both the spectral information of the multi-spectral image and the high spatial resolution information of the panchromatic image in a more effective way.

(3) Simultaneous localization and mapping (SLAM). Sensor fusion plays an essential role in solving the well-known SLAM problems (c.f. [110]). One of the greatest obstacles of using SLAM in a real-world environment is the need to maintain the full correlation structure between the vehicle and all of the landmark estimates. This structure is computationally expensive to maintain, and is not robust to linearization errors [35]. To circumvent this difficulty, a CI-based SLAM was developed in [35].

(4) Environmental monitoring [111]. Real-time environmental monitoring of pollutant dispersion due to chemical leaks is an essential task in disaster prevention. Hence, there is a great need to constantly estimate the characteristics of interest to evaluate the current hazardous level [111]. For example, CI was applied to the estimation of the concentration of the pollutants based on the measurements from a dynamically cooperating sensor vehicles [111].

7. Conclusion and Future Remarks

This overview gives a roadmap of the development and advances in multi-sensor fusion with unknown correlations (UCs). We start with the root causes of UCs. Next, the development of various methods to deal with UCs has been reviewed. Based on the nature of UCs, these approaches are effectively classified into two groups, namely, fusion under fully UCs and fusion under partially UCs. In particular, in the first group, the CI fusion rule has been reviewed rigorously in terms of its generalization, improvements, and applications. Furthermore, we notice that there has been an intense study on fusion with UCs in a distributed way. We have categorized and reviewed these results in terms of three groups, i.e., consensus-based CI, diffusion-based CI, and GCI-based multi-object tracking.

To conclude this overview, a glimpse of future perspectives are outlined in the following that may provide some research ideas in the area of information fusion under UCs.

(1) Other types of partially unknown correlations (PUCs). In Section 4, we summarized several typical types of PUCs, and reviewed the fusion methods in dealing with them. However, according to the cross-correlations [112, Equation (26)]:

We believe that there are other types of PUCs remaining to be studied. From Equation (26), it is obvious that the unknown sources can come from the uncertain system matrices  and  [113], uncertain-covariance noise  [114], or/and uncertain Kalman gains  (may be caused by unknown observation covariance [115]), which may be tackled by incorporating the existing techniques such as robust filtering [116], extended Kalman filtering [117], non-fragile filtering [118], and  filtering [119], etc.

(2) Explicit characterization of UCs. Owing to its complex unknown nature, when UCs appear, most of the results simply label the error cross-covariance  as unknown without mentioning the specific structures, which will inevitably lead to a certain degree of conservatism in the final fusion results [8]. It is worth noting that [51] made a first few attempts by providing an explicit characterization in terms of representation , where  is an unknown mutual covariance with its algebraic expression determined by an optimization solution. However, this method may come with the inconsistent estimates [3] and the hardly satisfied common prior estimate issues [52]. Therefore, it is meaningful to continue to improve the existing method by overcoming these weak points or develop new explicit characterization of UCs in the future.

(3) Two-stage fusion strategy. For the efficiency consideration, the implementation of CI-like fusion may be divided into two stages: off-line stage and on-line stage. In this setting, the computation burden caused by weight optimization can be shifted to the off-line design stage. Next, the optimized weighting parameters are adopted into the online implementation of fusion algorithms. Following this philosophy, [71] used the observability Grammian to search for the desired weights during the off-line stage, and provided the expectation that optimization methods such as linear matrix inequalities [75] may be helpful to find more suitable weights in varied situations.

(4) Robust fusion under unknown correlations. A prerequisite of CI is that estimates to be fused are consistent so as to guarantee consistency of data fusion. However, in practice, a different situation may arise when estimates from different nodes are determined to be mutually inconsistent [28]. To handle this problem, [28] proposed a covariance union method using a Mahalanobis distance to detect the statistical difference between estimates. If the threshold for the Mahalanobis distance is crossed, the estimates are deemed incoherent. Furthermore, [6] introduced an adaptive parameter that can be used to robustly fuse estimates with various mixtures of incoherency. However, determining this threshold is not straightforward in general. The multivariate statistical monitoring methods [120] may provide new insights into finding more appropriate thresholds.

(5) Stability issues of fusion under unknown correlations. Recently, there has been a renewed activity in the study of the stability issues of fusion under unknown correlations. To be more specific, the corresponding observability or detectability issues with following conditions have been reported, i.e., partial local uniform observability [16], minimal nodes uniform observability [121], collective observability [24], global observability [86], collectively uniform detectability [70], weightedly uniform detectability [97] and jointly uniform observability [71] conditions. These conditions extend the traditional observability [122,123] or detectability [124,125] conditions such that they are more suitable in a sensor fusion setting, where the system can be unobservable or undetectable from a standalone node point of view. As a result, it is interesting to find out how those observability or detectability conditions can be utilized to enhance the fusion performance.

Funding: This work was partially supported by the National Natural Science Foundation of China (Grant 62103283).

Conflicts of Interest: The authors declare no conflict of interest.

References

  1. Hall, D.L.; Llinas, J. An introduction to multisensor data fusion. Proc. IEEE, 1997, 85: 6−23.
  2. Chen, L.J.; Arambel, P.O.; Mehra, R.K. Estimation under unknown correlation: Covariance intersection revisited. IEEE Trans. Autom. Control, 2002, 47: 1879−1882.
  3. Reinhardt, M.; Noack, B.; Arambel, P.O.; et al. Minimum covariance bounds for the fusionunder unknown correlations. IEEE Signal Process. Lett., 2015, 22: 1210−1214.
  4. Bar-Shalom, Y.; Campo, L. The effect of the common process noise on the two-sensor fused-track covariance. IEEE Trans. Aerosp. Electron. Syst. 1986, AES-22, 803–805. doi: 10.1109/TAES.1986.310815.
  5. Julier, S.J.; Uhlmann, J.K. A non-divergent estimation algorithm in the presence of unknown correlations. In Proceedings of the 16th American Control Conference, Albuquerque, 06 June 1997; IEEE: Albuquerque, 1997; pp. 2369–2373. doi: 10.1109/ACC.1997.609105.
  6. Wang, Y.M.; Li, X.R. Distributed estimation fusion with unavailable cross-correlation. IEEE Trans. Aerosp. Electron. Syst., 2012, 48: 259−278.
  7. Uhlmann, J.K. General data fusion for estimates with unknown cross covariances. In Proceedings of SPIE 2755, Signal Processing, Sensor Fusion, and Target Recognition V, Orlando, 14 June 1996; SPIE: Orlando, 1996; p. 2755. doi: 10.1117/12.243195.
  8. Li, W.Y.; Wang, Z.D.; Wei, G.L.; et al. A survey on multi-sensor fusion and consensus filtering for sensor networks. Discrete Dyn. Nat. Soc., 2015, 2015: 683701.
  9. Gao, Y.X.; Li, X.R.; Song, E.B. Robust linear estimation fusion with allowable unknown cross-covariance. IEEE Trans. Syst. Man Cybernet. Syst., 2016, 46: 1314−1325.
  10. Wu, Z.Z.; Cai, Q.Q.; Fu, M.Y. Covariance intersection for partially correlated random vectors. IEEE Trans. Automat. Control, 2018, 63: 619−629.
  11. Olfati-Saber, R.; Murray, R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Automat. Control, 2004, 49: 1520−1533.
  12. Ren, W.; Beard, R.W.; Atkins, E.M. Information consensus in multivehicle cooperative control. IEEE Control Syst. Mag., 2007, 27: 71−82.
  13. Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and cooperation in networked multi-agent systems. Proc. IEEE, 2007, 95: 215−233.
  14. He, W.L.; Xu, B.; Han, Q.L.; et al. Adaptive consensus control of linear multiagent systems with dynamic event-triggered strategies. IEEE Trans. Cybernet., 2020, 50: 2996−3008.
  15. Cattivelli, F.S.; Sayed, A.H. Diffusion strategies for distributed Kalman filtering and smoothing. IEEE Trans. Automat. Control, 2010, 55: 2069−2084.
  16. Hu, J.W.; Xie, L.H.; Zhang, C.S. Diffusion Kalman filtering based on covariance intersection. IEEE Trans. Signal Process., 2012, 60: 891−902.
  17. Fantacci, C.; Vo, B.N.; Vo, B.T.; et al. Robust fusion for multisensor multiobject tracking. IEEE Signal Process. Lett., 2018, 25: 640−644.
  18. Uhlmann, J.K. Dynamic Map Building and Localization: New Theoretical Foundations. Ph.D. Thesis, University of Oxford, Oxford, 1995.
  19. Hurley, M.B. An information theoretic justification for covariance intersection and its generalization. In Proceedings of the 5th International Conference on Information Fusion, Annapolis, 08–11 July 2002; IEEE: Annapolis, 2002; pp. 505–511. doi: 10.1109/ICIF.2002.1021196.
  20. Taylor, C.N.; Bishop, A.N. Homogeneous functionals and bayesian data fusion with unknown correlation. Information Fusion, 2019, 45: 179−189.
  21. Bailey, T.; Julier, S.; Agamennoni, G. On conservative fusion of information with unknown non-Gaussian dependence. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 09–12 July 2012; IEEE: Singapore, 2012; pp. 1876–1883. doi: 10.1016/j.inffus.2018.02.002.
  22. Grime, S.; Durrant-Whyte, H.F. Data fusion in decentralized sensor networks. Control Eng. Pract., 1994, 2: 849−863.
  23. Makarenko, A.; Brooks, A.; Kaupp, T.; et al. Decentralised data fusion: A graphical model approach. In Proceedings of the 12th International Conference on Information Fusion, Seattle, 06–09 July 2009; IEEE: Seattle, 2009; pp. 545–554.
  24. Battistelli, G.; Chisci, L. Kullback–Leibler average, consensus on probability densities, and distributed state estimation with guaranteed stability. Automatica, 2014, 50: 707−718.
  25. Julier, S.J. An empirical study into the use of chernoff information for robust, distributed fusion of gaussian mixture models. In Proceedings of the 2006 9th International Conference on Inf. Fusion, Florence, 10–13 July 2006; IEEE: Florence, 2006. doi: 10.1109/ICIF.2006.301755.
  26. Li, T.C.; Corchado, J.M.; Sun, S.D. On generalized covariance intersection for distributed PHD filtering and a simple but better alternative. In Proceedings of the 20th International Conference on Information Fusion, Xi'an, 10–13 July 2017; IEEE: Xi'an, 2017. doi: 10.23919/ICIF.2017.8009732.
  27. Farrell, W.J.; Ganesh, C. Generalized chernoff fusion approximation for practical distributed data fusion. In Proceedings of the 12th International Conference on Information Fusion, Seattle, 06–09 July 2009; IEEE: Seattle, 2009; pp. 555–562.
  28. Uhlmann, J.K. Covariance consistency methods for fault-tolerant distributed data fusion. Inf. Fusion, 2003, 4: 201−215.
  29. Friedman, N. Seapower as Strategy: Navies and National Interests; Naval Institute Press: Annapolis, 2001.
  30. Chang, K.; Chong, C.Y.; Mori, S. Analytical and computational evaluation of scalable distributed fusion algorithms. IEEE Trans. Aerosp. Electron. Syst., 2010, 46: 2022−2034.
  31. Chong, C.Y.; Mori, S. Convex combination and covariance intersection algorithms in distributed fusion. In Proceedings of the 4th International Conference on Information Fusion, Montreal; Montreal, 2001. Available online:https://www.semanticscholar.org/paper/Convex-Combination-and-Covariance-Intersection-in-Chong/184648882646f20062bf8f4fd0514ccd82253978 (accessed on15 October 2022)
  32. Welch, G.; Bishop, G. SCAAT: Incremental tracking with incomplete information. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, New York, August 1997; Addison-Wesley Publishing Co: New York, 1997; pp. 333–344. doi: 10.1145/258734.258876.
  33. Zhu, H.Y.; Zhai, Q.Z.; Yu, M.W.; et al. Estimation fusion algorithms in the presence of partially known cross-correlation of local estimation errors. Inf. Fusion, 2014, 18: 187−196.
  34. Battistelli, G.; Chisci, L.; Mugnai, G.; et al. Consensus-based linear and nonlinear filtering. IEEE Trans. Automat. Control, 2015, 60: 1410−1415.
  35. Julier, S.J.; Uhlmann, J.K. Using covariance intersection for SLAM. Robot. Auton. Syst., 2007, 55: 3−20.
  36. Niehsen, W. Information fusion based on fast covariance intersection filtering. In Proceedings of the 5th International Conference on Information Fusion, Annapolis, 08–11 July 2002; IEEE: Annapolis, 2002; pp. 901–904. doi: 10.1109/ICIF.2002.1020907.
  37. Clarke, D. Minimum information loss fusion in distributed sensor networks. In 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, 05–08 July 2016; IEEE: Heidelberg, 2016; pp. 1057–1062.
  38. Mahler, R.P.S. Optimal/robust distributed data fusion: A unified approach. In Proceedings of SPIE 4052, Signal Processing, Sensor Fusion, and Target Recognition IX, Orlando, 4 August 2000; SPIE: Orlando, 2000. doi: 10.1117/12.395064.
  39. Wang, Y.M.; Li, X.R. Distributed estimation fusion under unknown cross-correlation: An analytic center approach. In Proceedings of the 2010 14th International Conference on Information Fusion, Edinburgh, 26–29 July 2010; IEEE: Edinburgh, 2010. doi: 10.1109/ICIF.2010.5711989.
  40. Wu, T.T.; An, J.; Ding, C.S.; Luo, S.X. Research on ellipsoidal intersection fusion method with unknown correlation. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 09–12 July 2012; IEEE: Singapore, 2012; pp. 558–564.
  41. Deng, Z.L.; Zhang, P.; Qi, W.J.; et al. Sequential covariance intersection fusion Kalman filter. Inf. Sci., 2012, 189: 293−309.
  42. Ajgl, J.; Straka, O. A geometrical perspective on fusion under unknown correlations based on Minkowski sums. In Proceedings of the 2017 20th International Conference on Information Fusion, Xi'an, 10–13 July 2017; IEEE: Xi'an, 2017. doi: 10.23919/ICIF.2017.8009722.
  43. Ajgl, J.; Straka, O. Covariance intersection in track-to-track Fusion: Comparison of fusion configurations. IEEE Trans. Ind. Inf., 2018, 14: 1127−1136.
  44. Deng, Z.L.; Zhang, P.; Qi, W.J.; et al. The accuracy comparison of multisensor covariance intersection fuser and three weighting fusers. Inf. Fusion, 2013, 14: 177−185.
  45. Üney, M.; Clark, D.E.; Julier, S.J. Distributed fusion of PHD filters via exponential mixture densities. IEEE J. Sel. Top. Signal Process., 2013, 7: 521−531.
  46. Ahmed, N.R.; Campbell, M. Fast consistent Chernoff fusion of Gaussian mixtures for ad hoc sensor networks. IEEE Trans. Signal Process., 2012, 60: 6739−6745.
  47. Gunay, M.; Orguner, U.; Demirekler, M. Chernoff fusion of Gaussian mixtures based on sigma-point approximation. IEEE Trans. Aerosp. Electron. Syst., 2016, 52: 2732−2746.
  48. Benaskeur, A.R. Consistent fusion of correlated data sources. In Proceedings of 28th Annual Conference of the Industrial Electronics Society, Seville, 05–08 November 2002; IEEE: Seville, 2002; pp. 2652–2656. doi: 10.1109/IECON.2002.1182812.
  49. Zhou, Y.; Li, J.X. Data fusion of unknown correlations using internal ellipsoidal approximation. IFAC Proc. Vol., 2008, 41: 2856−2860.
  50. Vazhentsev, A.Y. On internal ellipsoidal approximations for problems of control synthesis with bounded coordinates. J. Computer Syst. Sci. Int., 2000, 39: 399−406.
  51. Sijs, J.; Lazar, M. State fusion with unknown correlation: Ellipsoidal intersection. Automatica, 2012, 48: 1874−1878.
  52. Ajgl, J.; Straka, O. On weak points of the ellipsoidal intersection fusion. In Proceedings of 2017 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Daegu, 16–18 November 2017; IEEE: Daegu, 2017. doi: 10.1109/MFI.2017.8170403.
  53. Noack, B.; Sijs, J.; Reinhardt, M.; et al. Decentralized data fusion with inverse covariance intersection. Automatica, 2017, 79: 35−41.
  54. Noack, B.; Sijs, J.; Hanebeck, U.D. Inverse covariance intersection: New insights and properties. In Proceedings of the 20th International Conference on Information Fusion, Xi'an, 10–13 July 2017; IEEE: Xi'an, 2017. doi: 10.23919/ICIF.2017.8009694.
  55. Yang, F.W.; Li, Y.M. Set-membership filtering for systems with sensor saturation. Automatica, 2009, 45: 1896−1902.
  56. Bakr, M.A.; Lee, S. Track level fusion with an estimation of maximum bound of unknown correlation. In Proceedings of 2016 International Conference on Control, Automation and Information Sciences (ICCAIS), Ansan, 27–29 October 2016; IEEE: Ansan, 2016. doi: 10.1109/ICCAIS.2016.7822431.
  57. Leonardos, S.; Daniilidis, K. A game-theoretic approach to robust fusion and kalman filtering under unknown correlations. In Proceedings of the 36th American Control Conference, Seattle, 24–26 May 2017; IEEE: Seattle, 2017. doi: 10.23919/ACC.2017.7963339.
  58. Zhang, X.H. An optimal data fusion algorithm in the presence of unknown cross covariances. IEEE Trans. Automat. Control, 2020, 65: 1226−1233.
  59. Shirsat, A.; Mishra, S.; Zhang, W.L.; et al. Probabilistic consensus on feature distribution for multi-robot systems with Markovian exploration dynamics. IEEE Robot. Autom. Lett., 2022, 7: 6407−6414.
  60. Li, W.L.; Jia, Y.M. Distributed estimation for Markov jump systems via diffusion strategies. IEEE Trans. Aerosp. Electron. Syst., 2017, 53: 448−460.
  61. Franken, D.; Hupper, A. Improved fast covariance intersection for distributed data fusion. In Proceedings of the 7th International Conference on Information Fusion, Philadelphia, 25–28 July 2005; IEEE: Philadelphia, 2005. doi: 10.1109/ICIF.2005.1591849.
  62. Cong, J.L.; Li, Y.Y.; Qi, G.Q.; et al. An order insensitive sequential fast covariance intersection fusion algorithm. Inf. Sci. 2016, 367–368, 28–40. doi: 10.1016/j.ins.2016.06.001.
  63. Reinhardt, M.; Noack, B.; Hanebeck, U.D. Closed-form optimization of covariance intersection for low-dimensional matrices. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 09–12 July 2012; IEEE: Singapore, 2012; pp. 1891–1896.
  64. Xiao, L.; Boyd, S.; Lall, S. A scheme for robust distributed sensor fusion based on average consensus. In Proceedings of 4th International Symposium on Information Processing in Sensor Networks, Boise, 15 April 2005; IEEE: Boise, 2005; pp. 63–70. doi: 10.1109/IPSN.2005.1440896.
  65. Li, W.Y.; Wei, G.L.; Han, F.; et al. Weighted average consensus-based unscented Kalman filtering. IEEE Trans. Cybernet., 2016, 46: 558−567.
  66. Battistelli, G.; Chisci, L.; Fantacci, C. Parallel consensus on likelihoods and priors for networked nonlinear filtering. IEEE Signal Process. Lett., 2014, 21: 787−791.
  67. Battistelli, G.; Chisci, L. Stability of consensus extended Kalman filter for distributed state estimation. Automatica, 2016, 68: 169−178.
  68. Liu, Q.Y; Wang, Z.D.; He, X.; et al. On Kalman-consensus filtering with random link failures over sensor networks. IEEE Trans. Automat. Control, 2018, 63: 2701−2708.
  69. Wang, B.L.; Yi, W.; Hoseinnezhad, R.; et al. Distributed fusion with multi-bernoulli filter based on generalized covariance intersection. IEEE Trans. Signal Process., 2017, 65: 242−255.
  70. Li, W.Y.; Wang, Z.D.; Ho, D.W.C.; et al. On boundedness of error covariances for Kalman consensus filtering problems. IEEE Trans. Automat. Control, 2020, 65: 2654−2661.
  71. Li, W.Y.; Yang, F.W.; Wei, G.L. A novel observability gramian-based fast covariance intersection rule. IEEE Signal Process. Lett., 2018, 25: 1570−1574.
  72. Julier, S.J.; Uhlmann, J.K. General decentralized data fusion with covariance intersection (CI). In Handbook of Data Fusion. CRC Press, 2001. Available online:https://www.taylorfrancis.com/chapters/edit/10.1201/9781420053098-19/general-decentralized-data-fusion-covariance-intersection-simon-julier-jeffrey-uhlmann (accessed on 14 October 2022)
  73. Hanebeck, U.D.; Briechle, K.; Horn, J. A tight bound for the joint covariance of two random vectors with unknown but constrained cross-correlation. In Proceedings of the Conference Documentation International Conference on Multisensor Fusion and Integration for Intelligent Systems, Baden-Baden, 20–22 August 2001; IEEE: Baden-Baden, 2001. doi: 10.1109/MFI.2001.1013513.
  74. Reece, S.; Roberts, S. Robust, low-bandwidth, multi-vehicle mapping. In Proceedings of the 2005 7th International Conference on Information Fusion, Philadelphia, 25–28 July 2005; IEEE: Philadelphia, 2005. doi: 10.1109/ICIF.2005.1592009.
  75. Boyd, S.; El Ghaoui, L.; Feron, E.; et al. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, 1994; p. 15.
  76. Kaplan, L.M.; Blair, W.D.; Bar-Shalom, Y. Simulations studies of multisensor track association and fusion methods. In Proceedings of 2006 IEEE Aerospace Conference, Big Sky, 04–11 March 2006; IEEE: Big Sky. doi: 10.1109/AERO.2006.1655913.
  77. Qu, X.M.; Zhou, J.; Song, E.B.; Zhu, Y.M. Minimax robust optimal estimation fusion in distributed multisensor systems with uncertainties. IEEE Signal Process. Lett., 2010, 17: 811−814.
  78. Ajgl, J.; Straka, O. Rectification of partitioned covariance intersection. In Proceedings of the 38th American Control Conference, Philadelphia, 10–12 July 2019; IEEE: Philadelphia, 2019; pp. 5786–5791. doi: 10.23919/ACC.2019.8814466.
  79. Petersen, A.; Beyer, M.A. Partitioned covariance intersection. In Proceedings of International Symposium Information on Ships, 2001. Available online:https://scholar.google.co.jp/scholar?hl=en&as_sdt=0%2C5&as_vis=1&q=Partitioned+covariance+intersection&btnG= (accessed on 16 October 2022)
  80. Chen, B.; Hu, G.Q.; Ho, D.W.C.; et al. Distributed covariance intersection fusion estimation for cyber-physical systems with communication constraints. IEEE Trans. Automat. Control, 2016, 61: 4020−4026.
  81. Battistelli, G.; Chisci, L.; Selvi, D. A distributed kalman filter with event-triggered communication and guaranteed stability. Automatica, 2018, 93: 75−82.
  82. Chang, T.K.; Mehta, A. Control-theoretical and topological analysis of covariance intersection based distributed Kalman filter. IEEE Control Syst. Lett., 2018, 2: 665−670.
  83. Wang, S.C.; Ren, W. On the convergence of distributed estimation of LTV dynamic system with switching directed topologies and time-varying sensing models. In Proceedings of the 2016 35th American Control Conference, Boston, 06–08 July 2016; IEEE: Boston, 2016. doi: 10.1109/ACC.2016.7526522.
  84. Wang, S.C.; Ren, W. On the consistency and confidence of distributed dynamic state estimation in wireless sensor networks. In Proceedings of 54th IEEE Conference on Decision and Control (CDC), Osaka, 15–18 December 2015; IEEE: Osaka, 2015; pp. 3069–3074. doi: 10.1109/CDC.2015.7402680.
  85. Wang, S.C.; Ren, W. On the convergence conditions of distributed dynamic state estimation using sensor networks: A unified framework. IEEE Trans. Control Syst. Technol., 2018, 26: 1300−1316.
  86. He, X.K.; Xue, W.C.; Fang, H.T. Consistent distributed state estimation with global observability over sensor network. Automatica, 2018, 92: 162−172.
  87. Olfati-Saber, R. Distributed Kalman filtering for sensor networks. In Proceedings of 46th IEEE Conference on Decision and Control, New Orleans, 12–14 December 2007; IEEE: New Orleans, 2007; pp. 5492–5498. doi: 10.1109/CDC.2007.4434303.
  88. Wei, G.L.; Li, W.Y.; Ding, D.R.; Liu, Y.R. Stability analysis of covariance intersection-based Kalman consensus filtering for time-varying systems. IEEE Trans. Syst. Man Cybernet. Syst., 2020, 50: 4611−4622.
  89. Battistelli, G.; Chisci, L.; Morrocchi, S.; et al. An information-theoretic approach to distributed state estimation. IFAC Proc. Vol., 2011, 44: 12477−12482.
  90. Olfati-Saber, R.; Shamma, J.S. Consensus filters for sensor networks and distributed sensor fusion. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, 15 December 2005; IEEE: Seville, 2005; pp. 6698–6703. doi: 10.1109/CDC.2005.1583238.
  91. Olfati-Saber, R. Distributed Kalman filter with embedded consensus filters. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, 15 December 2005; IEEE: Seville, 2005; pp. 8179–8184. doi: 10.1109/CDC.2005.1583486.
  92. Olfati-Saber, R. Kalman-consensus filter: Optimality, stability, and performance. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, 15–18 December 2009; IEEE: Shanghai, 2009. doi: 10.1109/CDC.2009.5399678.
  93. Shen, B.; Wang, Z.D.; Hung, Y.S. Distributed H∞-consensus filtering in sensor networks with multiple missing measurements: The finite-horizon case. Automatica, 2010, 46: 1682−1688.
  94. Ugrinovskii, V. Distributed robust filtering with H∞ consensus of estimates. Automatica, 2011, 47: 1−13.
  95. Han, F.; Wei, G.L.; Ding, D.R.; et al. Local condition based consensus filtering with stochastic nonlinearities and multiple missing measurements. IEEE Trans. Automat. Control, 2017, 62: 4784−4790.
  96. Kamgarpour, M.; Tomlin, C. Convergence properties of a decentralized Kalman filter. In Proceedings of 2008 47th IEEE Conference on Decision and Control, Cancun, 09–11 December 2008; IEEE: Cancun, 2008; pp. 3205–3210. doi: 10.1109/CDC.2008.4738989.
  97. Li, W.Y.; Wei, G.L.; Ho, D.W.C.; et al. A weightedly uniform detectability for sensor networks. IEEE Trans. Neural Networks Learn. Syst., 2018, 29: 5790−5796.
  98. Battistelli, G.; Chisci, L.; Fantacci, C.; et al. Consensus-based multiple-model Bayesian filtering for distributed tracking. IET Radar Sonar Navigat., 2014, 9: 401−410.
  99. Yang, H.J.; Li, H.; Xia, Y. Q; et al. Distributed kalman filtering over sensor networks with transmission delays. IEEE Trans. Cybernet., 2021, 51: 5511−5521.
  100. Lopes, C.G.; Sayed, A.H. Diffusion least-mean squares over adaptive networks: Formulation and performance analysis. IEEE Trans. Signal Process., 2008, 56: 3122−3136.
  101. Tu, S.Y.; Sayed, A.H. Diffusion strategies outperform consensus strategies for distributed estimation over adaptive networks. IEEE Trans. Signal Process., 2012, 60: 6217−6234.
  102. Uney, M.; Clark, D.E.; Julier, S.J. Information measures in distributed multitarget tracking. In Proceedings of the 14th International Conference on Information Fusion, Chicago, 5–8 July 2011; IEEE: Chicago, 2011.
  103. Clark, D.; Julier, S.; Mahler, R.; et al. Robust multi-object sensor fusion with unknown correlations. In Proceedings of the Sensor Signal Processing for Defence (SSPD 2010), London, 29–30 September 2010; IET: London, 2010. doi: 10.1049/ic.2010.0233.
  104. Battistelli, G.; Chisci, L.; Fantacci, C.; et al. Consensus CPHD filter for distributed multitarget tracking. IEEE J. Sel. Top. Signal Process., 2013, 7: 508−520.
  105. Vo, B.T.; Vo, B.N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process., 2013, 61: 3460−3475.
  106. Li, H.; Nashashibi, F.; Yang, M. Split covariance intersection filter: Theory and its application to vehicle localization. IEEE Trans. Intellig. Transp. Syst., 2013, 14: 1860−1871.
  107. Lazarus, S.B.; Ashokaraj, I.; Tsourdos, A.; et al. Vehicle localization using sensors data fusion via integration of covariance intersection and interval analysis. IEEE Sensors J., 2007, 7: 1302−1314.
  108. Guo, Q.; Chen, S.Y.; Leung, H.; et al. Covariance intersection based image fusion technique with application to pansharpening in remote sensing. Inf. Sci., 2010, 180: 3434−3443.
  109. Shi, Y.; Yang, X.Y.; Cheng, T. Pansharpening of multispectral images using the nonseparable framelet lifting transform with high vanishing moments. Inf. Fusion, 2014, 20: 213−224.
  110. Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Automat. Mag., 2006, 13: 99−110.
  111. Ritter, T.; Euler, J.; Ulbrich, S.; et al. Decentralized dynamic data-driven monitoring of atmospheric dispersion processes. Proc. Computer Sci., 2016, 80: 919−930.
  112. Bar-Shalom, Y. On the track-to-track correlation problem. IEEE Trans. Automat. Control, 1981, 26: 571−572.
  113. Yang, F.W.; Wang, Z.D.; Hung, Y.S. Robust Kalman filtering for discrete time-varying uncertain systems with multiplicative noises. IEEE Trans. Automat. Control, 2002, 47: 1179−1183.
  114. Dong, Z.; You, Z. Finite-horizon robust kalman filtering for uncertain discrete time-varying systems with uncertain-covariance white noises. IEEE Signal Process. Lett., 2006, 13: 493−496.
  115. Wang, Y.L.; Djurić, P.M. Distributed Bayesian estimation of linear models with unknown observation covariances. IEEE Trans. Signal Process., 2016, 64: 1962−1971.
  116. Zhou, K.M.; Doyle, J.C.; Glover, K. Robust and Optimal Control; Prentice Hall: Upper Saddle River, 1995.
  117. Hu, J.; Wang, Z.D.; Gao, H.J.; et al. Extended kalman filtering with stochastic nonlinearities and multiple missing measurements. Automatica, 2012, 48: 2007−2015.
  118. Yang, G.H.; Wang, J.L. Robust nonfragile Kalman filtering for uncertain linear systems with estimator gain uncertainty. IEEE Trans. Automat. Control, 2001, 46: 343−348.
  119. Doyle, J.; Glover, K.; Khargonekar, P.; et al. State-space solutions to standard H2 and H∞ control problems. IEEE Trans. Automat. Control, 1989, 34: 831−847.
  120. Raich, A.; Çinar, A. Diagnosis of process disturbances by statistical distance and angle measures. Comput. Chem. Eng., 1997, 21: 661−673.
  121. Li, W.Y.; Yang, F.W.; Thiel, D.V.; et al. Minimal number of sensor nodes for distributed kalman filtering. IEEE Trans. Syst. Man Cybernet. Syst., 2022, 52: 1778−1786.
  122. Deyst, J.; Price, C. Conditions for asymptotic stability of the discrete minimum-variance linear estimator. IEEE Trans. Automat. Control, 1968, 13: 702−705.
  123. Li, W.Y.; Wei, G.L.; Ding, D.R.; et al. A new look at boundedness of error covariance of Kalman filtering. IEEE Trans. Syst. Man Cybernet. Syst., 2018, 48: 309−314.
  124. Anderson, B.D.O.; Moore, J.B. Detectability and stabilizability of time-varying discrete-time linear systems. SIAM J. Control Optimizat., 1981, 19: 20−32.
  125. Li, W.Y.; Wei, G.L.; Yang, F.W. Uniform detectability-aided boundedness analysis of error covariances of kalman filter for time-varying systems. IEEE Trans. Syst. Man Cybernet. Syst., 2022, 52: 4798−4806.