Adaptive Neural Event-Triggered Output-Feedback Optimal Tracking Control for Discrete-Time Pure-Feedback Nonlinear Systems

2.1. High-Order Neural Network

Article

Adaptive Neural Event-Triggered Output-Feedback Optimal Tracking Control for Discrete-Time Pure-Feedback Nonlinear Systems

Wei Wang ¹, and Min Wang ^1,2,*

¹ School of Automation Science and Engineering, South China University of Technology, Guangzhou 510641, China

² Pengcheng Laboratory, Shenzhen 518055, China

^* Correspondence: auwangmin@scut.edu.cn

Received: 20 December 2023

Accepted: 30 January 2024

Published: 26 June 2024

Abstract: In this article, a novel event-triggered (ET) output-feedback optimal tracking control scheme is developed for a class of uncertain discrete-time nonlinear systems in the pure-feedback form with immeasurable states. Firstly, different from the traditional n-step-ahead input-output prediction model, the immeasurable states of the system are estimated in real time by designing a neural network (NN) state observer. Then, the implicit function theorem and the mean value theorem are combined to tackle the nonaffine terms. The variable substitution approach is applied to overcome the causal contradiction problem during the backstepping design, and meanwhile the n-step time delays caused by the traditional n-step-ahead prediction model are avoided. Subsequently, the critic NN and the action NN are employed to minimize the system long-term performance measure. Under the adaptive critic design framework, an optimal controller is designed to obtain the optimal control performance. Furthermore, an ET mechanism is embedded between sensors and controllers to reduce network burden. A novel ET condition is developed to save network resources and guarantee the desired tracking control performance. According to the Lyapunov stability analysis, all the closed-loop system signals are guaranteed to be uniformly ultimately bounded.

1. Introduction

Over the past few decades, the control design problem for a class of uncertain lower triangular nonlinear systems has attracted extensive attention. In reality, abundant actual plants can be constructed as lower triangular nonlinear systems, such as mechanical systems [1], marine surface vessels [2], unmanned aerial vehicles [3] and robotic manipulators [4]. To handle the uncertain nonlinear functions presented in dynamical systems, adaptive neural networks (NNs) or/and fuzzy-logic systems have been widely employed in engineering practice owning to their universal approximation abilities [5, 6]. Based on the function approximator and backstepping technique, plenty of effective control schemes have been developed for uncertain nonlinear systems in various fields, such as state constraints [7], input constraints [8], actuator faults [9], and predefined performance [10]. These works are mostly based on the continuous-time (CT) strict-feedback nonlinear systems, while the control design problem of pure-feedback nonlinear systems is more complicated due to the existence of unknown nonaffine functions [11]. With the development of computer technology and digital control, the studies of discrete-time nonlinear systems have become a hot topic [12]. Compared with CT affine nonlinear systems, the control design for discrete-time pure-feedback nonlinear (DTPFN) systems is usually more challenging, and there exist rarely research works for DTPFN systems.

For discrete-time nonlinear systems, the causal contradiction problem is difficult to overcome during the controller design procedure via the backstepping technique [13]. The designed controller typically requires the future system signals which are unavailable in practice. In [14], the causal contradiction problem was effectively overcomed by transforming the original system into the n-step-ahead prediction model. In [15], based on the implicit function theorem and the mean value theorem, a DTPFN system was transformed into the n-step-ahead input-output prediction model to tackle the causal contradiction problem and immeasurable system states. According to the n-step-ahead prediction model, a lot of important works have been developed for discrete-time nonlinear systems [16−18]. However, there are still two limitations in these works: the process noise and measurable noise are not considered in the closed-loop system, and the n-step time delays exist in the transformed system. To overcome these two limitations, a variable substitution approach was proposed in [19] to solve the causal contradiction problem, which simplifies the controller design and avoids the n-step time delays. So far, the variable substitution approach has been mainly employed to solve the control design problem for discrete-time strict-feedback nonlinear systems. Nevertheless, there are few results for the control design of DTPFN systems based on the variable substitution approach because of the uncertain nonaffine terms. In [20], by combining the implicit function theorem and the mean value theorem, the variable substitution approach was applied to design an ET optimal tracking control scheme for a class of second-order DTPFN systems.

With the development of information science and wireless communication technology, network-based control has been widely applied in solving the remote control problem [21−24]. The system signals are transmitted from sensors to controllers or from controllers to actuators by means of communication network. For increasingly complex control tasks, a large number of system signals are transmitted through communication network, which will increase network burden. Due to limited network resources, some undesirable phenomena may occur, such as transmission delays [25], packet loss [26], disorders [27], and network attacks [28, 29]. To save network resources and reduce network burden, an event-triggered control (ETC) scheme was developed in [30]. Different from the traditional time-triggered control (TTC) technique, system signals are transmitted from sensors to controllers only when the presented event-triggered (ET) condition is satisfied. Based on the ET mechanism, many meaningful works were proposed for CT nonlinear systems [31−33]. In [34], an ET optimal controller was designed for CT nonlinear systems based on reinforcement learning. In [35, 36], the ETC scheme was further extended to multi-agent systems. On the basis of the n-step-ahead prediction model, there exist many valuable ETC research works for discrete-time nonlinear systems [37−39]. However, these works need to calculate n intermediate ET conditions and n virtual control laws. In order to save computation resources and simplify the ET condition, a novel ETC scheme was proposed in [40] for discrete-time nonlinear systems by the variable substitution approach. In practice, the states of some physical systems are immeasurable because of sensor limitations [41−43]. Based on the neural state observer and the variable substitution approach, an ET adaptive neural control scheme has been proposed in [44, 45] for discrete-time strict-feedback systems with known constant gains. Until now, the neural state observer of DTPFN systems has never been considered in existing literature because of coupling.

In modern industry, optimal control can obtain better control performance and make the cost of the controller smaller. Dynamic programming is an effective technique to solve optimization problems, but it may cause ``curse of dimensionality" for high-order systems [46]. In order to solve the difficulty, an adaptive critic design (ACD) scheme was proposed in [47] to design the optimal controller based on the critic-action NN structure, where the system long-term performance measure was considered to obtain the optimal control performance. There exist a lot of optimal control works for nonlinear systems which are required to satisfy the matching condition [48−50]. Based on the ACD framework and backstepping technique, many important works have been reported for nonlinear systems with the mismatching condition in different phenomena, such as state constraints [51], dead-zone [52], actuator faults [53], and unknown backlashlike hysteresis [54]. However, the existing optimal research works are mostly based on state feedback and TTC. It is challenging to develop the ET output-feedback optimal tracking control scheme for DTPFN systems with immeasurable states and limited network resources.

According to the above discussions, the design problem of ET output-feedback optimal tracking control is addressed in this paper for a class of uncertain DTPFN systems. Firstly, an NN-based state observer is constructed to estimate the immeasurable system states. Then, the variable substitution approach is applied to overcome the causal contradiction problem during backstepping procedure, which avoids the n-step time delays. The implicit function theorem and mean value theorem are combined to tackle the nonaffine terms. In order to obtain the optimal control performance, an ACD framework is constructed to design the optimal tracking controller. A critic-action NN structure is constructed to minimize the long-term performance measure. Moreover, an ET mechanism is embedded between sensors and controllers. A novel ET condition is presented to save network resources and guarantee the stability of the closed-loop system. The proposed optimal control scheme guarantees the optimal tracking control performance, estimates the immeasurable system states, and reduces network burden. To be more specific, the main contributions of this paper are highlighted as follows.

1) A neural state observer is constructed to estimate the immeasurable system states, which decouples the designed observer and controller. Based on the observer states and ET mechanism, the actual controller is designed to guarantee the tracking control performance. According to state estimation errors and tracking errors, a novel ET condition is designed to save network resources, which improves transient control performance and reduces unnecessary triggered events in steady-state process.

2) By combining the implicit function theorem and mean value theorem, the variable substitution approach is employed to overcome the causal contradiction problem for uncertain DTPFN systems during the backstepping design procedure. The proposed scheme avoids the n-step time delays caused by the traditional n-step-ahead prediction model.

3) The ACD framework is developed to design an optimal controller, which guarantees the optimal tracking control performance. To obtain the action NN weight updating laws, the variable substitution approach is applied to transform the unknown term into the available signal iteratively, which is effective to implement the optimal controller.

2. Problem Formulation and Preliminaries

In this paper, the optimal tracking control problem of an uncertain DTPFN system with immeasurable states is considered as follows:

\( \left\{\begin{array}{l} {x_{i}(k+1)=f_{i}\left(\bar{x}_{i}(k), x_{i+1}(k)\right), i=1,2, \cdots, n-1 }\\{x_{n}(k+1)=f_{n}\left(\bar{x}_{n}(k), u(k), d(k)\right)} \\{y(k)=x_{1}(k)} \end{array}\right. \) (1)

where \( \bar{x}_i(k)=[x_1(k),\cdots,x_i(k)]^T\in \Re^i \) for \( i=1,2,...n \) are system state vectors, \( u(k) \in \Re \) and \( y(k) \in \Re \) are ststem control input and output, respectively. \( f_i(\cdot) \) are unknown nonlinear functions for \( i=1,2,\cdots n \). \( d(k) \) is the bounded external disturbance and satisfies \( |d(k)| \leq \bar{d} \) with \( \bar{d} \) being a positive constant. Only the system output can be obtained and the system states are assumed to be immeasurable.

The system uncertain nonlinear functions \( f_{i}(\cdot, \cdot): R^{i} \times R \rightarrow R \), \( i=1,2, \cdots, n-1 \), and \( f_{n}(\cdot, \cdot, \cdot): R^{n} \times R \times R \rightarrow R \) are continuous with respect to all the arguments and continuously differentiable with respect to the second argument.

For the convenience of theoretical analysis, define the following nonlinear functions:

\( \left\{\begin{array}{l} g_{i}(\cdot)=\partial f_{i}\left(\bar{x}_{i}(k), x_{i+1}(k)\right) / \partial x_{i+1}(k), i=1,2, \cdots, n-1 \\ g_{n}(\cdot)=\partial f_{n}\left(\bar{x}_{n}(k), u(k), d(k)\right) / \partial u(k). \end{array}\right. \) (2)

There exist two positive constants \( 0<\underline{g}_{i}<\bar{g}_{i} \) such that \( \underline{g}_{i} \leq \left|g_{i}(\cdot)\right| \leq \bar{g}_{i} \), \( i=1,2, \cdots, n \).

Without loss of generality, it is supposed that the signs of \( g_{i}(\cdot) \) are all positive. To simplify the notation, define \( \underline{g}=\prod_{i=1}^{n} \underline{g}_{i} \) and \( \bar{g}=\prod_{i=1}^{n} \bar{g}_{i} \).

The system function \( f_{n}\left(\bar{x}_{n}(k), u(k), d(k)\right) \) is a Lipschitz function with respect to \( d(k) \). There exists a positive constant \( L_{d} \) such that

\( \begin{split} d_s(k) =& \left|f_{n}\left(\bar{x}_{n}(k), u(k), d_{1}(k)\right)-f_{n}\left(\bar{x}_{n}(k), u(k), d_{2}(k)\right)\right| \\ &\leq L_{d}\left|d_{1}(k)-d_{2}(k)\right|. \end{split} \) (3)

Remark 1: Adaptive nerual output-feedback control scheme was proposed in [15, 18] for uncertain DTPFN systems by transforming the original system into the n-step-ahead input-output prediction model. The transformed system containes the current and past disturbances. Moreover, the original system functions are required to satisfy the Lipschitz condition. In this paper, by employing the variable substitution approach, it is unnecessary to assume that all the system functions satisfy the Lipschitz condition, which relaxes the restrictions of the closed-loop system. Additionally, the controller is directly designed in the original system without system transformation. Thus, the past disturbances will not appear in the system function.

In this paper, a high-order neural network (HONN) is applied to approximate the uncertain nonlinear function \( f(\xi(k)) \) on a compact set \( \Omega \) as follows:

\( f(\xi(k))=W^{*T}\Phi(\xi(k))+\varepsilon(\xi(k)) \) (4)

where \( \xi(k)=[\xi_1(k),\xi_2(k),\cdots,\xi_n(k)]^{T} \in \Omega \in \Re^{n} \) is the input vector, \( W^{*} \in \Re^{l} \) is the ideal constant weight vector, \( l \) is the number of neurons, \( \varepsilon(\xi(k)) \) is the approximation error, and \( \Phi(\xi(k))=[\phi_1(\xi(k)),\phi_2(\xi(k)),\cdots,\phi_l(\xi(k))]^{T} \) is the basis function vector. In the HONN, \( \phi_{i}(\xi(k))=\prod_{j \in I_{i}}[\phi(\xi_{j}(k))]^{p_{j}^{i}} \), \( i=1,2,\cdots, l \), \( j=1,2,\cdots, n \), where \( \{I_{1},I_{2},\cdots, I_{l}\} \) is a collection of \( l \) not-ordered subsets of \( \{1,2,\cdots, n\} \), \( \phi(\xi_j(k))=\tanh(\xi_{j}(k)) \), and \( p_{j}^{i} \) is a non-negative integer. According to the universal approximation property of the HONN, if \( l \) is selected to be sufficiently large, the approximation error \( \varepsilon(\xi(k)) \) satisfies \( |\varepsilon(\xi(k))|<\bar \epsilon,\forall{\xi(k) \in \Omega \in \Re^{n}} \), where \( \bar \epsilon \) is an arbitrarily small positive constant.

The basis function vector \( \Phi(\xi(k)) \) satisfies the local Lipschitz condition. There exists a positive constant \( L_s \) such that \( ||\Phi(\xi_1(k))-\Phi(\xi_2(k))||\leq L_s||\xi_1(k)-\xi_2(k)|| \).

\( \Phi^{T}(\xi(k)) \Phi(\xi(k))<l. \) (5)

2.2. Event-Triggered Mechanism

Since the system states are assumed to be immeasurable, an NN-based state observer is employed to estimate the immeasurable states. As displayed in Figure 1, the estimated states \( \hat{x}(k) \) are transmitted from the observer to controller through communication network. In order to reduce network burden and save network resources, an ET mechanism is employed and the ET condition is duly designed.

Figure 1. The event-triggered block diagram of the closed-loop system.

The triggering instants are defined by \( k_0=0<k_1<k_2<\cdots<k_\infty \). Let \( \{k_s\}_{s=0}^\infty \) denote the sequence of triggering instants, which is a subsequence of the time sequence \( \{k,k \in \mathbb{N}\} \). The observer states \( \hat{x}(k) \) are transmitted to the controller only when the ET condition is satisfied. To guarantee the tracking control performance of the uncertain closed-loop system, a Zero-Order Holder (ZOH) is employed to keep the last transmitted signals \( \hat{x}(k_s) \) during the triggering interval \( k_s<k<k_{s+1} \). The transmitted signals \( \hat{x}(k_s) \) is used to calculate the optimal controller \( u(k) \).

To design the ET condition, define the ET error based on the current estimated states \( \hat{x}(k) \) and the last transmitted states \( \hat{x}(k_s) \) as follows:

\( \Delta(k)= \left\{\begin{array}{*{20}{l}} {0, }& {k=k_{s} }\\{\hat{x}(k)-\hat{x}(k_{s}), }& {k_s<k<k_{s+1}} \\ \end{array}\right. \) (6)

where \( \Delta(k)=[\Delta_1(k),\Delta_2(k),\cdots,\Delta_n(k)]^T \), \( \Delta_i(k)=\hat{x}_{i}(k)-\hat{x}_{i}(k_{s}) \) for \( i=1,2,\cdots,n \).

3. NN-Based State Observer Design

In this section, an NN-based state observer is designed to estimate the immeasurable system states \( x(k) \). To design the state observer, define the following functions:

\( \left\{\begin{array}{l} {F_{i}\left(\bar{x}_{i}(k), x_{i+1}(k)\right) = f_{i}\left(\bar{x}_{i}(k), x_{i+1}(k)\right) - g_i x_{i+1}(k)}\\ { F_{n}\left(\bar{x}_{n}(k), u(k)\right) = f_{n}\left(\bar{x}_{n}(k), u(k),0\right)}\\ { d_o(k)=f_{n}\left(\bar{x}_{n}(k), u(k),d(k)\right) - f_{n}\left(\bar{x}_{n}(k), u(k),0\right)} \end{array}\right. \) (7)

where \( g_i \) is the designed constant, \( i=1,2, \cdots, n-1 \). According to Assumption 3, \( d_o(k) \) is bounded and satisfies \( |d_o(k)| \leq L_d d(k) \leq L_d \bar{d} := \bar d_o \). Then, the DTPFN system (1) is transformed into the following form:

\( \left\{\begin{array}{l}{x_{i}(k+1)=F_{i}\left(\bar{x}_{i}(k), x_{i+1}(k)\right) + g_i x_{i+1}(k)}\\{x_{n}(k+1)=F_{n}\left(\bar{x}_{n}(k), u(k)\right) + d_o(k)}\\{y(k)=x_{1}(k),i=1,2, \cdots, n-1. }\end{array}\right. \) (8)

The HONNs with \( l_i \) neurons are employed to approximate the unknown nonlinear functions \( F_i(\cdot) \) as follows:

\( \left\{\begin{array}{l}{F_{i}\left(\bar{x}_{i}(k), x_{i+1}(k)\right) = \Theta_{i}^{* T} \Phi_{i}\left(\bar{x}_{i+1}(k)\right)+\varepsilon_{i}(k)}\\{F_{n}\left(\bar{x}_{n}(k), u(k)\right) = \Theta_{n}^{* T} \Phi_{n}\left(\bar{x}_{n}(k),u(k)\right)+\varepsilon_{n}(k)}\end{array}\right. \) (9)

where \( \Theta_{i}^{*} \) is the ideal weight vector and the approximation error \( \varepsilon_{i}(k) \) satisfies \( |\varepsilon_{i}(k)| \leq \bar \varepsilon_{i} \), \( i=1,2, \cdots, n \).

To estimate the immeasurable system states, an NN-based state observer is designed as follows:

\( \left\{ \begin{array}{l} \,{\hat{x}_i(k+1)= \hat{\Theta}^{T}_{i}(k)\Phi_i(\hat{\bar{x}}_{i+1}(k)) + g_i\hat{x}_{i+1}(k)+\kappa_i(\hat{x}_1(k)-y(k))}\\ {\hat{x}_n(k+1)= \hat{\Theta}^{T}_{n}(k)\Phi_n( \hat{\bar{x}}_n(k),u(k))+\kappa_n(\hat{x}_1(k)-y(k))} \end{array} \right. \) (10)

where \( \hat{x}_i(k) \) is the estimate of \( x_i(k) \), \( \hat{\bar{x}}_i(k)=[\hat{x}_1(k),\cdots,\hat{x}_i(k)]^{T}\in \Re^{i} \), \( \hat{\Theta}_{i}(k) \) is the estimate of \( \Theta_{i}^{*} \), \( \kappa_i>0 \) is design parameters. Let the state observer weight estimation error \( \tilde{\Theta}_i(k)=\hat{\Theta}_i(k)-\Theta^{*}_i \).

Define the state estimation error

\( \tilde{x}(k)=[\tilde{x}_1(k),\tilde{x}_2(k),\cdots,\tilde{x}_n(k)]^{T} \) (11)

where \( \tilde{x}_i(k)=\hat{x}_i(k)-x_i(k) \), \( i=1,2,...,n \). By combining system (8) with state observer (10), it has

\( \tilde{x}(k+1)=A\tilde{x}(k)+\tilde{\Theta}^{T}(k)\Phi(k)+\zeta(k) \) (12)

where \( \tilde{\Theta}^{T}(k)\Phi(k) = [\tilde{\Theta}_1^{T}(k)\Phi_1(\hat{\bar{x}}_{2}(k)),\cdots,\tilde{\Theta}_n^{T}(k)\Phi_n(\hat{\bar{x}}_n(k), \)\( u(k))]^{T} \), \( \zeta(k) = [\Theta_{1}^{* T}\left(\Phi_{1}\left(\hat{\bar{x}}_{2}(k)\right) - \Phi_{1}\left(\bar{x}_{2}(k)\right)\right) - \varepsilon_{1}(k),\cdots, \)\( \Theta_{n}^{* T}\left(\Phi_{n}\left(\hat{\bar{x}}_{n}(k),u(k)\right)-\Phi_{n}\left(\bar{x}_{n}(k),u(k)\right)\right)-\varepsilon_{n}(k)+d_o(k)]^{T} \) and

\( A=\left(\begin{array}{*{20}{c}} {\kappa_{1} } & { g_1 } & { ... } & { 0} \\{\vdots } & { \vdots } & { \ddots } & { \vdots }\\ {\kappa_{n-1} } & { 0 } & { \cdots } & { g_{n-1}} \\ {\kappa_{n} } & { 0 } & { \cdots } & { 0 } \end{array}\right). \)

The designed parameters \( g_i \) and \( \kappa_i \) are selected such that the matrix \( A \) is Schur stability. \( \zeta(k) \) is bounded and satisfies \( |\zeta(k)| \leq \sum_{i=1}^{n}\left(2\left\|\Theta_{i}^{*}\right\| \sqrt{l_{i}}+\bar{\varepsilon}_{i}\right)+\bar{d}_{o}:=\bar{\zeta} \). The state observer NN weights are updated by

\( \hat{\Theta}_i(k+1)=\hat{\Theta}_i(k)-\frac{\varrho_i \Phi_i(\hat{\bar{x}}_{i+1}(k))\tilde{x}_1(k)}{1+||\Phi_i(\hat{\bar{x}}_{i+1}(k))||^{2}\tilde{x}_1^2(k)}-\sigma_i\hat{\Theta}_i(k) \) (13)

where \( \varrho_i \) and \( \sigma_i \) are positive constants to be designed, \( i=1,2,\cdots,n \), \( \hat{{x}}_{n+1}(k) = u(k) \). According to \( \tilde{\Theta}_i(k)= \hat{\Theta}_i(k)-\Theta^{*}_i \), we have

\( \tilde{\Theta}_i(k+1)=\tilde{\Theta}_i(k)-\frac{\varrho_i \Phi_i(\hat{\bar{x}}_{i+1}(k))\tilde{x}_1(k)}{1+||\Phi_i(\hat{\bar{x}}_{i+1}(k))||^{2}\tilde{x}_1^2(k)}-\sigma_i\hat{\Theta}_i(k). \) (14)

Remark 2: Inspired by [19], the weight updating law of the neural state observer is designed as (13). In the paper, the input vector of the basis function vector is different from [19]. The observer NN weight updating law (13) is designed according to the Lyapunov stability analysis. From (13), the state observer NN weights can be guaranteed to be UUB.

To simplify the notation, we define

\( \vartheta_{i}(k)=\frac{\Phi_i(\hat{\bar{x}}_{i+1}(k))}{1+||\Phi_i(\hat{\bar{x}}_{i+1}(k))||^{2}\tilde{x}_1^2(k)}. \) (15)

\( \left\{\begin{array}{l} {1-2\sigma_{i} > 0} \\ \mu \sigma_{i}-\dfrac{\mu}{4 \beta_{i}}-4 l_{i}\|M\|>0 \\ 2A^{T}MA-M=-N. \end{array}\right. \) (16)

Proof of Theorem 1. To prove the convergence of the state estimation errors and the weight estimation errors, we consider the following Lyapunov function candidate:

\( V_o(k)=V_e(k) + \mu V_\Theta(k) \) (17)

with \( V_e(k)=\tilde{x}^{T}(k)M\tilde{x}(k) \) and \( V_\Theta(k)=\sum_{i=1}^{n}\tilde{\Theta}_i^T(k)\tilde{\Theta}_i(k) \).

According to the state estimate error system (12), the difference of \( V_e(k) \) is calculated as

\( \begin{split} \Delta V_{e}(k) =& \tilde{x}^{T}(k+1) M \tilde{x}(k+1)-\tilde{x}^{T}(k) M \tilde{x}(k) \\ &\leq \tilde{x}^{T}(k)\left(2 A^{T} M A-M\right) \tilde{x}(k)+2\|M\| \left\|\tilde{\Theta}^{T}(k) \Phi(k)+\zeta(k)\right\|^{2} \\&\leq -\tilde{x}^{T}(k) N \tilde{x}(k)+4\|M\| \sum_{i=1}^{n} l_{i}\left\|\tilde{\Theta}_{i}(k)\right\|^{2}+\aleph_{1} \end{split} \) (18)

where \( \aleph_{1}=4\|M\|\bar{\zeta}^2 \). Substituting (14) into the difference of \( V_\Theta(k) \) yields

\( \begin{split} \Delta V_\Theta (k)= &\sum_{i=1}^{n}\tilde{\Theta}_i^T(k+1)\tilde{\Theta}_i(k+1)-\sum_{i=1}^{n}\tilde{\Theta}_i^T(k)\tilde{\Theta}_i(k)\\ = &\sum_{i=1}^{n}\varrho_i^2\vartheta_{i}^T(k)\vartheta_{i}(k)\tilde{x}_1^2(k)-2\sum_{i=1}^{n}\sigma_i\tilde{\Theta}_i^{T}(k)\hat{\Theta}_i(k)+\sum_{i=1}^{n}\sigma_i^2\|\hat{\Theta}_i(k)\|^2 \\ &-2\sum_{i=1}^{n}\varrho_i\tilde{\Theta}_i^{T}(k)\vartheta_{i}(k)\tilde{x}_1(k)+2\sum_{i=1}^{n}\sigma_i\varrho_i\hat{\Theta}_i^T(k)\vartheta_{i}(k)\tilde{x}_1(k). \end{split} \) (19)

By combining the following equation

\( 2\tilde{\Theta}_i^T(k)\hat{\Theta}_i(k)=\tilde{\Theta}_i^T(k)\tilde{\Theta}_i(k)+\|\hat{\Theta}_i(k)\|^2-\|\Theta^{*}_i\|^2 \) (20)

and the following Young’s inequalities

\( \begin{align} \varrho_i^2\vartheta_{i}^T(k)\vartheta_{i}(k)\tilde{x}_1^2(k) \leq & \frac{\varrho_i^2}{4}\\ -2\varrho_{i}\tilde{\Theta}_{i}^{T}(k)\vartheta_{i}(k)\tilde{x}_1(k) \leq & \frac{\tilde{\Theta}^{T}(k) \tilde{\Theta}(k)}{4 \beta_{i}}+\beta_{i} \varrho_i^{2}\\ 2\sigma_i\varrho_i\hat{\Theta}_i^T(k)\vartheta_{i}(k)\tilde{x}_1(k) \leq & \sigma_{i}^{2}||\hat{\Theta}_{i}(k)||^{2}+\frac{\varrho_{i}^{2}}{4}\\ \end{align} \) (21)

we have

\( \Delta V_\Theta (k) \leq -\sum\limits_{i=1}^{n}\left(\sigma_{i}-\frac{1}{4 \beta_{i}}\right) \tilde{\Theta}_{i}^{T}(k) \tilde{\Theta}_{i}(k)-\sum\limits_{i=1}^{n} \sigma_{i}\left(1-2 \sigma_{i}\right) \hat{\Theta}_{i}^{T}(k) \hat{\Theta}_{i}(k)+\aleph_{2} \) (22)

where \( \aleph_{2}=\sum_{i=1}^{n} \sigma_{i}\left\|\Theta_{i}^{*}\right\|^{2}+\left(0.5+\beta_{i}\right) \varrho_{i}^{2} \). Combining (18) with (22), we have

\( \begin{split} \Delta V_{o}(k) = &\Delta V_{e}(k)+\mu \Delta V_{\Theta}(k) \\ &\leq -\sum_{i=1}^{n}\left(\mu \sigma_{i}-\frac{\mu}{4 \beta_{i}}-4 l_{i}\|M\|\right) \tilde{\Theta}_{i}^{T}(k) \tilde{\Theta}_{i}(k)-\tilde{x}^{T}(k) N \tilde{x}(k)+\aleph_{3} \end{split} \) (23)

where \( \aleph_{3}=\aleph_{1}+\mu \aleph_{2} \). From (23), if the condition (16) is satisfied, the state estimate errors and the observer NN weight estimate errors are UUB, i.e., \( ||\tilde{x}(k)||^{2}\leq \Xi_{ox}, ||\tilde{\Theta}_{i}(k)||^2\leq \Xi_{om} \).

Remark 3: An output-feedback tracking controller was proposed in [15] for the DTPFN system by transforming the original system into the n-step-ahead input-output prediction model, where the input and output are applied in controller design. However, the measurement noise and process noise cannot be appropriately handled since the system states cannot be observed in real time. To overcome this difficulty, a neural state observer is constructed in this section to estimate the unknown system states in real time.

4. ET Output-Feedback Optimal Tracking Controller Design

In this section, an ET output-feedback optimal tracking controller is constructed based on the variable substitution approach, the neural state observer (10), and the reinforcement learning strategy.

4.1. ET-based Controller Design

Based on the observer states, define the following coordinate transformations:

\( \left\{\begin{array}{l} {z_1(k)=x_1(k)-y_{d}(k)} \\ {z_i(k)=\hat{x}_i(k)-\alpha_{i-1}(k),i=2,\cdots,n }\end{array}\right. \) (24)

where \( y_{d}(k) \) is the reference trajectory, and \( \alpha_{i-1}(k) \), \( i=2,\cdots,n \), are virtual controllers to be designed later. From (24), one has \( x_i(k)=z_i(k)+\alpha_{i-1}(k)-\tilde{x}_i(k),i=2,\cdots,n \).

According to the system model (1) and coordinate transformation (24), the difference of \( z_1(k) \) is calculated as

\( \begin{align} z_{1}(k+1)= &x_1(k+1)-y_d(k+1)\\ = & f_{1}\left(\bar{x}_{1}(k), x_{2}(k)\right)-y_{d}(k+1). \end{align} \) (25)

Based on Assumption 2 and the implicit function theorem, there exists a virtual controller \( \alpha_{1}(k)=T_1(\bar{x}_{1}(k), y_d(k+1)) \) such that

\( f_{1}\left(\bar{x}_{1}(k), \alpha_{1}(k)\right)-y_{d}(k+1)=0. \) (26)

Consider (24), (25) with (26), one has

\( z_{1}(k+1)= f_{1}\left(\bar{x}_{1}(k), z_{2}(k)+\alpha_{1}(k)-\tilde{x}_{2}(k)\right)-f_{1}\left(\bar{x}_{1}(k), \alpha_{1}(k)\right). \) (27)

Based on the mean value theorem, it follows

\( z_{1}(k+1)=g_{1}\left(\bar{x}_{1}(k), x_{2}^{c}(k)\right)\left(z_{2}(k)-\tilde{x}_{2}(k)\right) \) (28)

where \( x_{2}^{c}(k) \in\left[\min \left\{{x}_{2}(k), \alpha_{1}(k)\right\}, \max \left\{{x}_{2}(k), \alpha_{1}(k)\right\}\right] \).

Noticing that \( z_2(k)=\hat{x}_2(k)-\alpha_1(k) \), the dynamic equation of \( z_2(k) \) is calculated as

\( \begin{align} z_{2}(k+1)= &\hat{x}_{2}(k+1)-\alpha_{1}(k+1)\\ = &f_{2}\left(\bar{x}_{2}(k), x_{3}(k)\right)-\alpha_{1}(k+1)+\tilde{x}_{2}(k+1). \end{align} \) (29)

From (29), the term \( \alpha_{1}(k+1) \) contains the future system state \( x_1(k+1) \), which causes the causal contradiction problem. Using the variable substitution approach, \( \alpha_{1}(k+1) \) can be represented as a function of the current system states

\( \begin{align} \alpha_{1}(k+1) & =T_{1}\left(\bar{x}_{1}(k+1), y_{d}(k+2)\right) \\ & =T_{1}\left(f_{1}\left(\bar{x}_{1}(k), x_{2}(k)\right), y_{d}(k+2)\right) \\ & :=H_{1}\left(\bar{x}_{2}(k), y_{d}(k+2)\right). \end{align} \) (30)

Based on the implicit function theorem, there exists a virtual controller \( \alpha_{2}(k)=T_2(\bar{x}_{2}(k),y_d(k+2)) \) such that

\( f_{2}\left(\bar{x}_{2}(k), \alpha_{2}(k)\right)-H_{1}\left(\bar{x}_{2}(k), y_{d}(k+2)\right)=0. \) (31)

Noticing (29), (30) and (31), we obtain

\( z_{2}(k+1)= f_{2}\left(\bar{x}_{2}(k), z_{3}(k)+\alpha_{2}(k)-\tilde{x}_{3}(k)\right)-f_{2}\left(\bar{x}_{2}(k), \alpha_{2}(k)\right) + \tilde{x}_{2}(k+1). \) (32)

Based on the mean value theorem, it follows

\( z_{2}(k+1)=g_{2}\left(\bar{x}_{2}(k), x_{3}^{c}(k)\right)\left(z_{3}(k)-\tilde{x}_{3}(k)\right) + \tilde{x}_{2}(k+1) \) (33)

where \( x_{3}^{c}(k) \in\left[\min \left\{{x}_{3}(k), \alpha_{2}(k)\right\}, \max \left\{{x}_{3}(k), \alpha_{2}(k)\right\}\right] \).

Due to \( z_i(k)=\hat{x}_i(k)-\alpha_{i-1}(k) \), its difference is calculated as

\( \begin{align} z_{i}(k+1)= &\hat{x}_{i}(k+1)-\alpha_{i-1}(k+1)\\ = &f_{i}\left(\bar{x}_{i}(k), x_{i+1}(k)\right)-\alpha_{i-1}(k+1)+\tilde{x}_{i}(k+1). \end{align} \) (34)

Using the variable substitution approach, \( \alpha_{i-1}(k+1) \) can be represented by the current system states

\( \begin{align} \alpha_{i-1}(k+1) & =T_{i-1}\left(\bar{x}_{i-1}(k+1), y_{d}(k+i)\right) \\ & =T_{i-1}\left(f_{1}\left(\cdot\right), \ldots, f_{i-1}\left(\cdot\right), y_{d}(k+i)\right) \\ & :=H_{i-1}\left(\bar{x}_{i}(k), y_{d}(k+i)\right). \end{align} \) (35)

Based on the implicit function theorem, there exists a virtual controller \( \alpha_{i}(k)=T_i(\bar{x}_{i}(k),y_d(k+i)) \) such that

\( f_{i}\left(\bar{x}_{i}(k), \alpha_{i}(k)\right)-H_{i-1}\left(\bar{x}_{i}(k), y_{d}(k+i)\right)=0. \) (36)

Consider (34), (35) with (36), we have

\( z_{i}(k+1)= f_{i}\left(\bar{x}_{i}(k), z_{i+1}(k)+\alpha_{i}(k)-\tilde{x}_{i+1}(k)\right)-f_{i}\left(\bar{x}_{i}(k), \alpha_{i}(k)\right) + \tilde{x}_{i}(k+1). \) (37)

Based on the mean value theorem, it follows

\( z_{i}(k+1)=g_{i}\left(\bar{x}_{i}(k), x_{i+1}^{c}(k)\right)\left(z_{i+1}(k)-\tilde{x}_{i+1}(k)\right) + \tilde{x}_{i}(k+1) \) (38)

where \( x_{i+1}^{c}(k) \in\left[\min \left\{{x}_{i+1}(k), \alpha_{i}(k)\right\}, \max \left\{{x}_{i+1}(k), \alpha_{i}(k)\right\}\right] \).

For \( z_{n}(k)=\hat{x}_{n}(k)-\alpha_{n-1}(k) \), its difference is calculated as

\( \begin{align} z_{n}(k+1)= &\hat{x}_{n}(k+1)-\alpha_{n-1}(k+1)\\ = &f_{n}\left(\bar{x}_{n}(k), u(k),d(k)\right)-\alpha_{n-1}(k+1)+\tilde{x}_{n}(k+1)\\ = &F_{n}\left(\bar{x}_{n}(k), u(k)\right)-\alpha_{n-1}(k+1)+\tilde{x}_{n}(k+1)+d_o(k).\\ \end{align} \) (39)

By similar analysis, the term \( \alpha_{n-1}(k+1) \) can be represented by the current system states

\( \begin{align} \alpha_{n-1}(k+1) & =T_{n-1}\left(\bar{x}_{n-1}(k+1), y_{d}(k+n)\right) \\ & =T_{n-1}\left(f_{1}\left(\cdot\right), \cdots, f_{n-1}\left(\cdot\right), y_{d}(k+n)\right) \\ & :=H_{n-1}\left(\bar{x}_{n}(k), y_{d}(k+n)\right). \end{align} \) (40)

Using the implicit function theorem, there exists an ideal controller \( u^{*}(k)=T_n(\bar{x}_{n}(k),y_d(k+n)) \) such that

\( F_{n}\left(\bar{x}_{n}(k), u^{*}(k)\right)-H_{n-1}\left(\bar{x}_{n}(k), y_{d}(k+n)\right)=0. \) (41)

Using (39), (40) with (41), one has

\( z_{n}(k+1)= F_{n}\left(\bar{x}_{n}(k), u(k)\right)-F_{n}\left(\bar{x}_{n}(k), u^{*}(k)\right)+\tilde{x}_{n}(k+1) + d_o(k). \) (42)

By the mean value theorem, it can be obtained that

\( z_{n}(k+1)= g_{n}\left(\bar{x}_{n}(k), u^{c}(k)\right)\left(u(k)-{u}^{*}(k)\right) + \tilde{x}_{n}(k+1)+d_o(k) \) (43)

where \( u^{c}(k) \in\left[\min \left\{u(k), u^*(k)\right\}, \max \left\{u(k), u^*(k)\right\}\right] \). Let \( g_{i}(k)=g_{i}\left(\bar{x}_{i}(k), x_{i+1}^{c}(k)\right),i=1,2,\cdots, n-1,g_{n}(k)= g_{n}(\bar{x}_{n}(k), u^{c}(k)) \).

As the nonlinear function \( T_n(\bar{x}_{n}(k),y_d(k+n)) \) is unknown and the ideal controller \( u^{*}(k) \) cannot be implemented directly to control the closed-loop system, an HONN is employed to approximate \( u^{*}(k) \) as follows:

\( u^{*}(k)=W_{a}^{*T}\Phi_a(\xi(k))+\varepsilon_a(\xi(k)) \) (44)

where \( W_{a}^{*} \) is the ideal weight vector, \( \varepsilon_a(k) \) is the approximation error with \( |\varepsilon_a(k)| \leq \bar\varepsilon_a \), and \( \xi(k)=[{x}^{T}(k), y_{d}(k+n)]^T \) is the HONN input vector.

In order to save communication network resources and reduce the transmission burden, the actual controller is designed as follows:

\( u(k)=\hat{W}_{a}^{T}(k)\Phi_{a}(\hat{\xi}(k_{s})) \) (45)

where \( \hat{W}_{a}(k) \) is the estimate of the ideal weight \( {W}_{a}^{*} \), \( \hat{\xi}(k_{s})=[\hat{x}^{T}(k_{s}),y_{d}(k+n)]^T \). Substituting (44) and (45) into (43) yields

\( \begin{align} z_{n}(k+1)= & g_{n}\left(k\right)\left[\hat{W}_{a}^{T}(k) \Phi_{a}\left(\hat{\xi}\left(k_{s}\right)\right)-W_{a}^{* T} \Phi_{a}(\xi(k))\right]-g_n(k)\varepsilon_{a}(k)+\tilde{x}_{n}(k+1)+d_{o}(k) \\ = & g_{n}\left(k\right)\left[\hat{W}_{a}^{T}(k)\left(\Phi_{a}\left(\hat{\xi}\left(k_{s}\right)\right)-\Phi_{a}(\hat{\xi}(k))\right)+\tilde{W}_{a}^{T}(k) \Phi_{a}(\hat{\xi}(k))\right] +\tilde{x}_{n}(k+1)+\varpi(k) \end{align} \) (46)

where \( \tilde{W}_{a}(k)=\hat{W}_{a}(k)-{W}_{a}^{*} \) is the weight estimation error, \( \varpi(k)=g_{n}(k) W_{a}^{* T}(\Phi_{a}(\hat{\xi}(k))-\Phi_{a}(\xi(k)))- g_{n}(k) \varepsilon_{a}(k)+ d_{o}(k) \) is a bounded term and satisfies \( |\varpi(k)| \leq \bar{g}_{n} L_{s} \Xi_{ox}\left\|W_{a}^{*}\right\|+\bar{g}_{n} \bar{\varepsilon}_{a}+\bar{d}_{o}:=\bar{\varpi} \). Let \( \Phi_{a}(k)=\Phi_{a}(\hat{\xi}(k)) \), \( \varphi_{a}(k)= \tilde{W}_{a}^{T}(k) \Phi_{a}(k) \).

Remark 4: To overcome the causal contradiction problem during the backstepping design procedure, the n-step-ahead prediction model was proposed in [14, 15] for discrete-time nonlinear systems, in which the n-step time delays exist duly. In [19], the variable substitution approach was developed to design the controller for discrete-time strict-feedback systems, where the n-step time delays were successfully avoided. So far, however, there have been few available results on the control design of DTPFN systems based on the variable substitution approach. In this section, the implicit function theorem and the mean value theorem are employed to handle the nonaffine terms. Different from the n-step-ahead prediction model [14, 15], the variable substitution approach is employed to overcome the causal contradiction problem for DTPFN systems without the system transformation.

4.2. Critic-Action Neural Networks Design

4.2.1. Critic Neural Network Design

The output of the critic neural network represents the long-term performance measure of system (1), which indicates the system tracking control performance. To describe the current system performance index, we define the utility function \( p(k) \) as follows:

\( p(k)=\left\{\begin{array}{l}{ 0,}\;{ if\; |z_1(k)|\leq \tau }\\ {1,}\;{\rm{otherwise}} \end{array}\right. \) (47)

where \( \tau \) is a positive parameter to be designed. The long-term performance measure \( J(k) \) is defined by

\( J(k)=\gamma^{N}p(k+1)+\gamma^{N-1}p(k+2)+\cdots +\gamma^{k+1}p(N)+ \cdots \) (48)

where \( 0<\gamma<1 \) is a discount factor, \( N \) is a positive integer and represents the horizon. According to (48), \( J(k) \) can be rewritten as the following form:

\( J(k)=\min\limits_{u(k)}\{\gamma J(k-1)-\gamma^{N+1}p(k)\}. \) (49)

Equation (49) is a Bellman equation. The function \( J(k) \) is unknown and difficult to be directly calculated, it can be approximated by a critic NN as follows:

\( J(k)=W_c^{*T} \Phi_{c}(\chi(k))+\varepsilon_c(\chi(k)) \) (50)

where \( W_c^{*} \) is the ideal weight vector, \( \chi(k)=[z_1(k),z_1(k-1),\cdots z_1(k-n+1)]^T \) is the input vector, and \( \varepsilon_c(\chi(k)) \) is the approximation error. Let \( \hat{W}_c(k) \) denotes the estimate of \( W_c^* \). The actual output of the critic NN is calculated as

\( \hat{J}(k)=\hat{W}_c(k)^T \Phi_{c}(\chi(k_s)). \) (51)

From (49), the critic NN error function \( e_c(k) \) is defined by

\( e_c(k)=\hat{J}(k)-\gamma(\hat{J}(k-1)-\gamma^N p(k)). \) (52)

Then, we can define the objective function of the critic NN to be minimized as follows:

\( E_c(k)=\frac{1}{2}e_c^2(k). \) (53)

Applying the ET mechanism and gradient descent method, the weight updating law for \( \hat{W}_c(k) \) is taken as

\( \hat{W}_c(k+1)=\hat{W}_c(k)+\eta(k)\Delta \hat{W}_c(k) \) (54)

with \( \Delta \hat{W}_c(k)=-\gamma_{c} {\partial E_c(k)}/{\partial \hat{W}_c(k)} \), where \( \gamma_{c} \) is the learning rate of the critic NN, and \( \eta(k) \) is the indicator function of the ET mechanism defined by

\( \eta(k)=\left\{\begin{array}{l} {1,}\;{if\; k=k_s }\\ {0,}\;{if\; k_s<k<k_{s+1}. } \end{array}\right. \) (55)

Combining (52), (53) and (54), we obtain

\( \hat{W}_c(k+1)= \hat{W}_c(k)-\eta(k)\gamma_{c} \Phi_{c}(\chi(k))[\hat{J}(k)-\gamma \hat{J}(k-1)+\gamma^{N+1}p(k)]. \) (56)

Let the weight estimate error be \( \tilde{W}_c(k)=\hat{W}_c(k)-W_c^* \). Subtracting \( W_c^{*} \) on both sides of (56) yields

\( \tilde{W}_c(k+1)= \tilde{W}_c(k)-\eta(k)\gamma_{c} \Phi_{c}(\chi(k))[\hat{J}(k)-\gamma \hat{J}(k-1)+\gamma^{N+1}p(k)]. \) (57)

Let \( \Phi_{c}(k)=\Phi_{c}\left(\chi\left(k_{s}\right)\right) \), \( \varphi_{c}(k)=\tilde{W}_{c}^{T}(k) \Phi_{c}(k) \).

4.2.2. Action Neural Network Design

The output of the action neural network is the actual controller \( u(k) \). The action NN is constructed to minimize the estimated system performance index function \( \hat{J}(k) \) and obtain the optimal tracking controller. The action NN error function is defined as follows:

\( e_a(k+n-1)=\frac{1}{\sqrt{g(k)}}(g(k)\tilde{u}(k)+\hat{J}(k)-J_h(k)) \) (58)

with \( g(k)=g_{n}(k) g_{n-1}(k+1) \cdots g_{1}(k+n-1) \) and \( \tilde{u}(k)=u(k)-u^{*}(k) \), where \( J_h(k) \) is the desired strategic utility function and the desired value for \( J_h(k) \) is \( ``0" \). Under Assumption 2, we can obtain \( 0<\underline{g} \leq g(k) \leq \bar{g} \).

The objective function of the action NN to be minimized is defined as

\( E_{a}(k+n-1)=\frac{1}{2} e_{a}^{2}(k+n-1). \) (59)

Based on the ET mechanism and gradient descent method, one has

\( \hat{W}_a(k+n)=\hat{W}_a(k)+\eta(k) \Delta \hat{W}_a(k) \) (60)

where \( \Delta \hat{W}_a(k)=-\gamma_a{\partial E_a(k+n-1)}/{\partial \hat{W}_a(k)} \), \( \gamma_{a} \) is the learning rate of the action NN. Combining (58), (58), and (60), we have

\( \hat{W}_a(k+n)= \hat{W}_a(k)-\eta(k)\gamma_{a}\Phi_{a}(\hat{\xi}(k))[g(k)\tilde u(k)+\hat{J}(k)]. \) (61)

Note that the weight updating law (61) cannot be directly implemented because \( g(k) \) and \( \tilde{u}(k) \) are unknown. To solve this problem, the variable substitution approach is employed to transform \( g(k)\tilde{u}(k) \) into the available signal. According to the error dynamic equation (43), it is obtained that

\( \tilde{u}(k)=\frac{z_{n}(k+1)-\tilde{x}_{n}(k+1)}{g_{n}(k)}-\frac{d_{o}(k)}{g_{n}(k)}. \) (62)

From (28), (33) and (38), it is derived that

\( \left\{\begin{array}{l} z_{2}(k)-\tilde{x}_{2}(k)=\dfrac{z_{1}(k+1)}{g_{1}(k)} \\ z_{i+1}(k)-\tilde{x}_{i+1}(k)=\dfrac{z_{i}(k+1)-\tilde{x}_{i}(k+1)}{g_{i}(k)}, \; \; i=2, \cdots, n-1. \end{array}\right. \) (63)

Combining (62) and (63), the following equation can be obtained iteratively by the variable substitution approach

\( \begin{align} \tilde{u}(k) & =\frac{z_{n-1}(k+2)-\tilde{x}_{n-1}(k+2)}{g_{n}(k) g_{n-1}(k+1)}-\frac{d_{o}(k)}{g_{n}(k)} \\ & =\frac{z_{n-2}(k+3)-\tilde{x}_{n-2}(k+3)}{g_{n}(k) g_{n-1}(k+1) g_{n-2}(k+2)}-\frac{d_{o}(k)}{g_{n}(k)} \\ & =\cdots \\ & =\frac{z_{1}(k+n)}{g(k)}-\frac{d_{o}(k)}{g_{n}(k)}. \end{align} \) (64)

Hence, it can be obtaind that \( g(k) \tilde{u}(k)=z_{1}(k+n)-g(k) d_{o}(k) / g_{n}(k) \) from (64). The term \( g(k) d_{o}(k) / g_{n}(k) \) is unknown and bounded, we employ \( z_{1}(k+n) \) instead of \( g(k) \tilde{u}(k) \). The weight updating law of the action NN (61) is further rewritten as

\( \hat{W}_a(k+n)= \hat{W}_a(k)-\eta(k)\gamma_{a}\Phi_{a}(\hat{\xi}(k))[z_1(k+n)+\hat{J}(k)]. \) (65)

It follows from (65) that

\( \tilde{W}_a(k+n)= \tilde{W}_a(k)-\eta(k)\gamma_{a}\Phi_{a}(\hat{\xi}(k))[z_1(k+n)+\hat{J}(k)]. \) (66)

The objective of the action NN is to minimize the estimated long-term performance measure and obtain the optimal controller. From (61), it is impossible to implement the action NN weight updating law because of the unknown nonlinear function \( g(k)\tilde{u}(k) \). In order to overcome this difficulty, the variable substitution approach is applied to transform \( g(k)\tilde{u}(k) \) into the available signal iteratively based on the error dynamic equations. From (65), the available action NN weight updating law is obtained to implement the optimal controller.

5. Stability Analysis

In order to save network resources and guarantee the tracking control performance of the closed-loop system, the ET mechanism is embedded between the observer and controller. Based on the ET error and the tracking error, a novel ET condition is designed as follows

\( k_{s+1}=\min \left\{k \in \mathbb{N} \mid k>k_{s},\|\Delta(k)\|^2>\frac{\Gamma z_{1}^2(k) + a}{b \left\|\hat{W}_{a}(k)\right\|^2+c}\right\} \) (67)

where \( b=4 q_{n} \bar{g}_{n}^{2} L_{s}^{2}, \Gamma, a, c, q_{n} \) are positive parameters to be designed. The parameter \( a \) can reduce unnecessary triggered events when the tracking error converges to the desired region. The parameter \( c \) can avoid the possible singularity problem and improve transient control performance.

Theorem 2. Consider the DTPFN system (1), the state observer (10) with the NN weight updating law (13), the critic NN (51) with the weight updating law (56), the action NN (45) with the weight updating law (61) and the event-triggered condition (67). The proposed control scheme guarantees all the closed-loop system signals are UUB if the design parameters satisfy the following condition:

\( \left\{\begin{array}{l} { q_{1}-\Gamma>0, q_{i}-3 q_{i-1} \bar{g}_{i-1}^{2}>0, i=2, \cdots, n }\\ { 1-\gamma_{c} l_{c}>0, \dfrac{1}{\bar{g}}-\gamma_{a} l_{a}>0, \lambda_{c}-2 \sigma_{c} \gamma^{2}>0 }\\ { \sigma_{c}-\lambda_{c}-\dfrac{3 \sigma_{a}}{\underline{g}}>0, \sigma_{a} \underline{g}-3 q_{n} \bar{g}_{n}^{2}>0. }\end{array}\right. \) (68)

Proof of Theorem 2. Choose the following Lyapunov function candidate:

\( V(k)=V_{1}(k)+V_{2}(k)+V_{3}(k)+V_{4}(k) \) (69)

where \( V_{1}(k)=\sum_{i=1}^{n} q_{i} z_{i}^{2}(k) \), \( V_{2}(k)=\dfrac{\sigma_{a}}{\gamma_{a}} \sum_{j=0}^{n-1} \tilde{W}_{a}^{T}(k+j) \tilde{W}_{a}(k+j) \), \( V_{3}(k)=\dfrac{\sigma_{c}}{\gamma_{c}} \tilde{W}_{c}^{T}(k) \tilde{W}_{c}(k) \), and \( V_{4}(k)=\lambda_{c}\|\varphi_{c} (k-1)\|^{2} \).

Under the designed event-triggered condition (67), the proof is divided into the following two cases.

At the triggering instants, the system data is transmitted from the observer to the controller via communication networks. Thus, one has \( \eta(k)=1 \). Based on the error dynamic equations (28), (33), (38), and (46), the difference of \( V_{1}(k) \) is calculated as

\( \begin{align} \Delta V_{1}(k)= & \sum_{i=1}^{n} q_{i}\left(z_{i}^{2}(k+1)-z_{i}^{2}(k)\right) \\ \leq & -q_{1} z_{1}^{2}(k)-\sum_{i=2}^{n}\left(q_{i}-3 q_{i-1} \bar{g}_{i-1}^{2}\right) z_{i}^{2}(k)+3 \sum_{i=2}^{n}\left(q_{i} \tilde{x}_{i}^{2}(k+1)+q_{i-1} \bar{g}_{i-1}^{2} \tilde{x}_{i}^{2}(k)\right) \\ & +3 q_{n} \bar{g}_{n}^{2} \varphi_{a}^{2}(k)+3 q_{n} \varpi^{2}(k). \end{align} \) (70)

Let \( \bar{q}=\max \left\{q_{1}, q_{2}, \cdots, q_{n}\right\} \). From condition (68), one has \( q_{i}>3 q_{i-1} \bar{g}_{i-1}^{2}, i=2, \cdots, n \). Then, it is clear from (70) that

\( \begin{align} \Delta V_{1}(k) \leq & -q_{1} z_{1}^{2}(k)-\sum_{i=2}^{n}\left(q_{i}-3 q_{i-1} \bar{g}_{i-1}^{2}\right) z_{i}^{2}(k)+3 \bar{q}\|\tilde{x}(k+1)\|^{2}+\bar{q}\|\tilde{x}(k)\|^{2}\\ &+3 q_{n} \bar{g}_{n}^{2} \varphi_{a}^{2}(k)+3 q_{n} \varpi^{2}(k) \\ \leq & -q_{1} z_{1}^{2}(k)-\sum_{i=2}^{n}\left(q_{i}-3 q_{i-1} \bar{g}_{i-1}^{2}\right) z_{i}^{2}(k)+3 q_{n} \bar{g}_{n}^{2} \varphi_{a}^{2}(k)+4 \bar{q} \Xi_{ox}+3 q_{n} \bar{\omega}^{2}. \end{align} \) (71)

According to the action NN weight error dynamic (66), we have

\( \Delta V_{2}(k) = \sigma_{a}\biggl[\gamma_{a}\left\|\Phi_{a}(k)\right\|^{2}\left(z_{1}(k+n)+\hat{J}(k)\right)^{2}-2 \varphi_{a}(k)\left(z_{1}(k+n)+\hat{J}(k)\right)\biggl]. \) (72)

It follows from (64) that

\( \begin{align} z_{1}(k+n) = &g(k)\left(\tilde{u}(k)+\frac{d_{o}(k)}{g_{n}(k)}\right) \\ = &g(k)\biggl(\varphi_{a}(k)+W_{a}^{* T}\left(\Phi_{a}(\hat{\xi}(k))-\Phi_{a}(\xi(k))\right)+\frac{d_{o}(k)}{g_{n}(k)}-\varepsilon_{a}(k)\biggl) \\ = &g(k)\left(\varphi_{a}(k)+\frac{\varpi(k)}{g_{n}(k)}\right). \end{align} \) (73)

Substituting (73) into (72) yields

\( \begin{align} \Delta V_{2}(k)= & \sigma_{a}\biggl[\gamma_{a}\left\|\Phi_{a}(k)\right\|^{2}\left(g(k) \varphi_{a}(k)+g(k) \frac{\varpi(k)}{g_{n}(k)}+\hat{J}(k)\right)^{2} \\ &-2 \varphi_{a}(k)\left(g(k) \varphi_{a}(k)+g(k) \frac{\varpi(k)}{g_{n}(k)}+\hat{J}(k)\right)\biggl]. \end{align} \) (74)

By the inequality \( q(x+y+z+w)^{2}-2x(x+y+z+w)\leq -(1-q)(x+y+z+w)^{2}+3y^{2}+3z^{2}+3w^{2}-x^{2} \), equation (74) can be rewritten as

\( \begin{align} \Delta V_{2}(k) \leq & -\sigma_{a}\left(\frac{1}{\bar{g}}-\gamma_{a}\left\|\Phi_{a}(k)\right\|^{2}\right)\left(z_{1}(k+n)+\hat{J}(k)\right)^{2} \\ & +3 \sigma_{a} \left( \bar{g} \frac{\bar{\varpi}^{2}}{\underline{g}_{n}^{2}}+\frac{\varphi_{c}^{2}(k)+\left\|W_{c}^{*}\right\|^{2} l_{c}}{\underline{g}}\right)-\sigma_{a} \underline{g} \varphi_{a}^{2}(k). \end{align} \) (75)

Consider the critic NN weight error system (57). The difference of \( V_{3}(k) \) is given by

\( \begin{align} \Delta V_{3}(k) \leq & -\sigma_{c}\Bigl(1-\gamma_{c}\left\|\Phi_{c}(k)\right\|^{2}\Bigl)\Bigl(\hat{J}(k)-\gamma \hat{J}(k-1)+\gamma^{N+1} p(k)\Bigl)^{2}\\ &-\sigma_{c}\left\|\varphi_{c}(k)\right\|^{2} +2 \sigma_{c} \gamma^{2}\left\|\varphi_{c}(k-1)\right\|^{2}+2 \sigma_{c}\left((1+\gamma)\left\|W_{c}^{*}\right\| \sqrt{l_{c}}+\gamma^{N+1}\right)^{2}. \end{align} \) (76)

For \( \Delta V_{4}(k) \), it is clear that

\( \Delta V_{4}(k)=\lambda_{c}\left\|\varphi_{c}(k)\right\|^{2}-\lambda_{c}\left\|\varphi_{c}(k-1)\right\|^{2}. \) (77)

For (68), (71), (75), (76), and (77), the difference of the Lyapunov function (69) is calculated as

\( \begin{align} \Delta V(k) \leq & -q_{1} z_{1}^{2}(k)-\sum_{i=2}^{n}\left(q_{i}-3 q_{i-1} \bar{g}_{i-1}^{2}\right) z_{i}^{2}(k)-\left(\sigma_{a} \underline{g}-3 q_{n} \bar{g}_{n}^{2}\right) \varphi_{a}^{2}(k)\\ &-\left(\sigma_{c}-\lambda_{c}-\frac{3 \sigma_{a}}{\underline{g}}\right) \varphi_{c}^{2}(k)-\left(\lambda_{c}-2 \sigma_{c} \gamma^{2}\right) \varphi_{c}^{2}(k-1)+D_{m 1} \end{align} \) (78)

where \( D_{m 1}=4 \bar{q} \Xi_{ox}+3 \sigma_{a} \bar{g} \dfrac{\bar{\varpi}^{2}}{\underline{g}_{n}^{2}}+\dfrac{3 \sigma_{a}\left\|W_{c}^{*}\right\|^{2} l_{c}}{\underline{g}}+3 q_{n} \bar{\varpi}^{2}+2 \sigma_{c}\left((1+\gamma)\left\|W_{c}^{*}\right\| \sqrt{l_{c}}+\gamma^{N+1}\right)^{2} \) is a bounded term. According to the Lyapunov stability theorem, all the closed-loop system signals are UUB at the triggering instants.

In Case 1, \( \varphi_{a}(k) \) and \( \varphi_{c}(k) \) are UUB, which means \( \tilde{W}_{a}(k) \) and \( \tilde{W}_{c}(k) \) are UUB at the triggering instants. In Case 2, \( \tilde{W}_{a}(k) \) and \( \tilde{W}_{c}(k) \) remain unchanged in the event-triggered intervals. Therefore, \( \tilde{W}_{c}(k) \) and \( \tilde{W}_{a}(k) \) are UUB over the entire time series. Then, we can obtain that \( \hat{W}_{a}(k) \) and \( \hat{W}_{c}(k) \) are also UUB. Because \( \eta(k)=0 \) during the event-triggered intervals, we have \( \Delta V_{2}(k)=0, \Delta V_{3}(k)=0 \). The difference of the Lyapunov function \( V(k) \) in Case 2 is given by

\( \begin{align} \Delta V(k) \leq & -q_{1} z_{1}^{2}(k)-\sum_{i=2}^{n}\left(q_{i}-3 q_{i-1} \bar{g}_{i-1}^{2}\right) z_{i}^{2}(k)+4 q_{n} \bar{g}_{n}^{2}\left\|\hat{W}_{a}^{T}(k)\left(\Phi_{a}\left(\hat{\xi}\left(k_{s}\right)\right)-\Phi_{a}(\hat{\xi}(k))\right)\right\|^{2}\\ &+4 q_{n} \bar{g}_{n}^{2} \varphi_{a}^{2}(k) +4 q_{n} \bar{\varpi}^{2}+5 \bar{q} \Xi_{ox} \\ \leq & -q_{1} z_{1}^{2}(k)-\sum_{i=2}^{n}\left(q_{i}-3 q_{i-1} \bar{g}_{i-1}^{2}\right) z_{i}^{2}(k)+4 q_{n} \bar{g}_{n}^{2} L_{s}^{2}\left\|\hat{W}_{a}(k)\right\|^{2}\|\Delta(k)\|^{2}+4 q_{n} \bar{g}_{n}^{2} \varphi_{a}^{2}(k)\\ &+4 q_{n} \bar{\varpi}^{2}+5 \bar{q} \Xi_{ox}. \end{align} \) (79)

Using the event-triggered condition (67), we have

\( \Delta V(k)\leq -\left(q_{1}-\Gamma\right) z_{1}^{2}(k)-\sum_{i=2}^{n}\left(q_{i}-3 q_{i-1} \bar{g}_{i-1}^{2}\right) z_{i}^{2}(k)+D_{m 2} \) (80)

where \( D_{m 2}=4 q_{n} \bar{g}_{n}^{2} \varphi_{a}^{2}(k)+4 q_{n} \bar{\varpi}^{2}+5 \bar{q} \Xi_{ox}+a \) is bounded. From (80), we can conclude that all system signals of the closed-loop systems are UUB during the event-triggered intervals.

According to the proof of two cases, all the closed-loop system signals are UUB over all sampling instants and the tracking error \( z_{1}(k) \) converges to a small neighborhood around the origin.

6. Simulation

In order to demonstrate the feasibility of the developed ET output-feedback optimal control scheme, the following uncertain DTPFN system is considered.

\( \left\{\begin{array}{l} {x_1(k+1)=f_1(\bar{x}_1(k),x_{2}(k)) }\\ {x_2(k+1)=f_2(\bar{x}_2(k),u(k)) +d(k)}\\ {y(k)=x_{1}(k) }\end{array}\right. \) (81)

where \( \bar{x}_2(k) \), \( y(k) \), and \( u(k) \) are the system state vector, system output, and control input, respectively. The unknown system nonlinear functions are chosen as

\( \begin{align} f_1(\bar{x}_1(k),x_{2}(k))&=\frac{0.2 x_{1}^{2}(k) x_{2}(k)}{1+x_{1}^{2}(k)}+0.5 x_{2}(k)\\ f_{2}(\bar{x}_{2}(k),u(k))&=\frac{x_{1}(k)}{1+x_{1}^{2}(k)+x_{2}^{2}(k)}+u(k)+0.2 \sin (u(k)).\nonumber \end{align} \)

The external disturbance is \( d(k) = 0.01 \cos (0.01 k) \cos \left(x_{1}(k)\right) \). The desired reference signal is \( y_{d}(k)=0.3 + 0.7 \sin (k T_{s} \text{π} / 2)+0.5 \sin (k T_{s} \pi) \) with the sampling period \( T_{s}=0.01 \). Considering the nonlinear system (81) and the neural state observer (10), the initial conditions are selected as \( x(0)=[0,0]^T \) and \( \hat{x}(0)=[0,0]^T \). The NN weights are initialized by \( \hat\Theta_{1}(0)=0.001,\hat\Theta_{2}(0)=0.001,\hat{W}_{c}(0)=0.001,\hat{W}_{a}(0)=0.001 \). By employing the trial-and-error method, the numbers of the observer NN nodes are \( l_{o1}=12 \) and \( l_{o2}=20 \), respectively. The numbers of the critic NN nodes and the action NN nodes are \( l_{c}=10 \) and \( l_{a}=10 \), respectively. The design parameters are selected as \( \kappa_{1}=-0.6 \), \( \kappa_{2}=-0.2 \), \( g_{1}=0.4 \), \( \varrho_{1}=0.058 \), \( \varrho_{2}=0.115 \), \( \sigma_{1}=0.001 \), \( \sigma_{2}=0.001 \), \( \tau=0.01 \), \( \gamma =0.65 \), \( \gamma_{c}=0.21 \), and \( \gamma_{a}=0.28 \). The ET threshold parameters are chosen as \( \Gamma=2.85 \), \( a=0.0022 \), \( b=1 \), and \( c=1.5 \).

Using the developed adaptive neural ET output-feedback optimal tracking control method, simulation results are displayed in Figures 2-9. From Figure 2, the system output \( y(k) \) tracks the desired reference signal \( y_{d}(k) \) and the tracking error \( z_1(k) \) converges to a small neighborhood around the origin. Figure 3 indicates the trajectories of the system states \( x(k) \) and the observer states \( \hat{x}(k) \). From Figure 3, the neural state observer can estimate the immeasurable system states well. Figure 4 represents the triggering intervals between two adjacent triggering instants. Based on the ET mechanism, the number of total triggering instants is 1537, which saves approximately \( 48.8\% \) of network resources. Figure 5 displays the actual control input \( u(k) \) and the estimated system long-term performance measure \( \hat{J}(k) \). From Figure 6, it is obvious that the norms of the state observer weights are bounded. Figure 7 indicates that the weights of the critic NN and the action NN are UUB. According to Figures 2-7, all the closed-loop system signals are guaranteed to be UUB during the entire time instants.

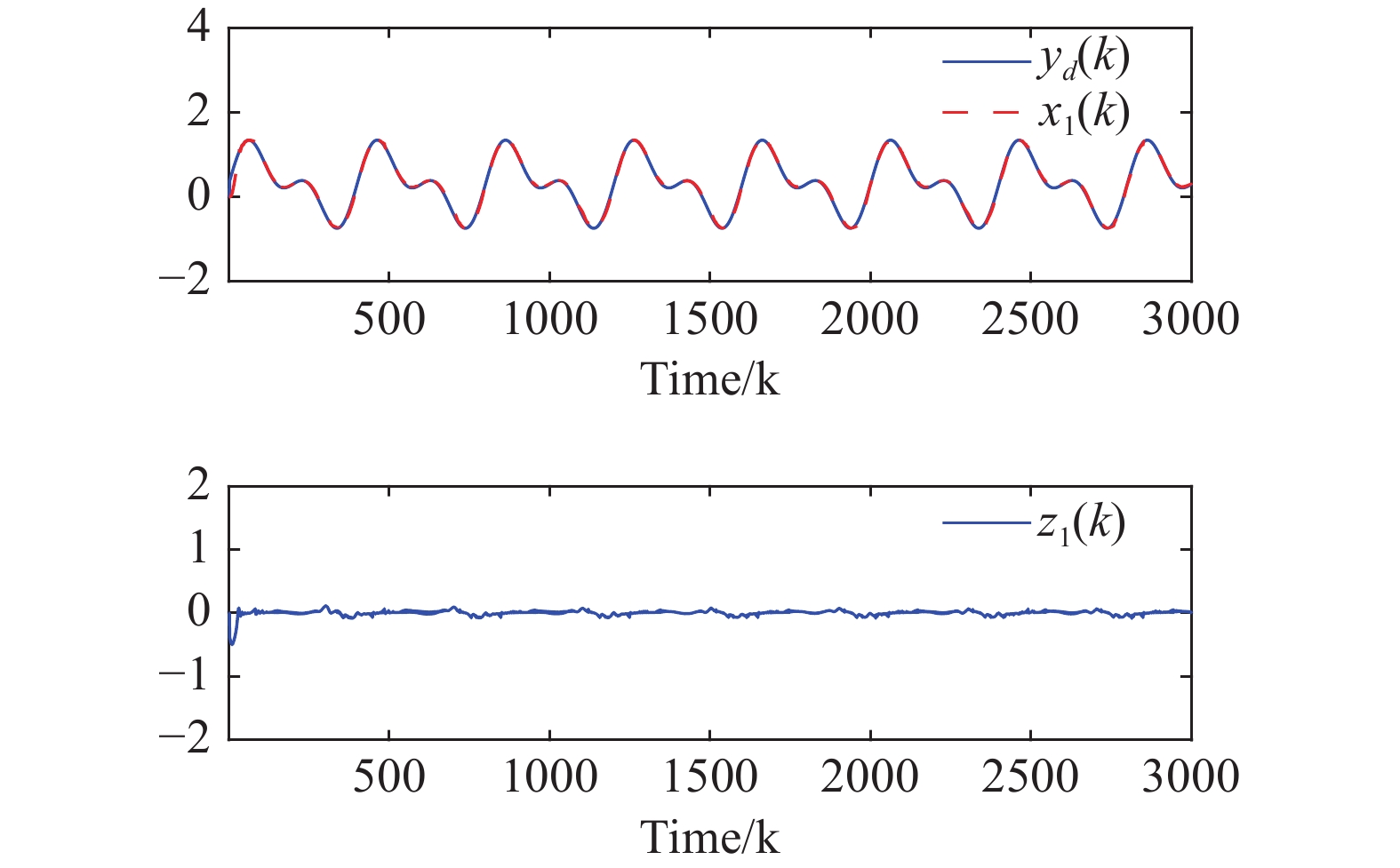
Figure 2. System output \( y(k) \), the reference signal \( y_{d}(k) \), and the tracking error \( z_{1}(k) \).

Figure 3. The trajectories of the system states \( x(k) \) and the observer states \( \hat{x}(k) \).

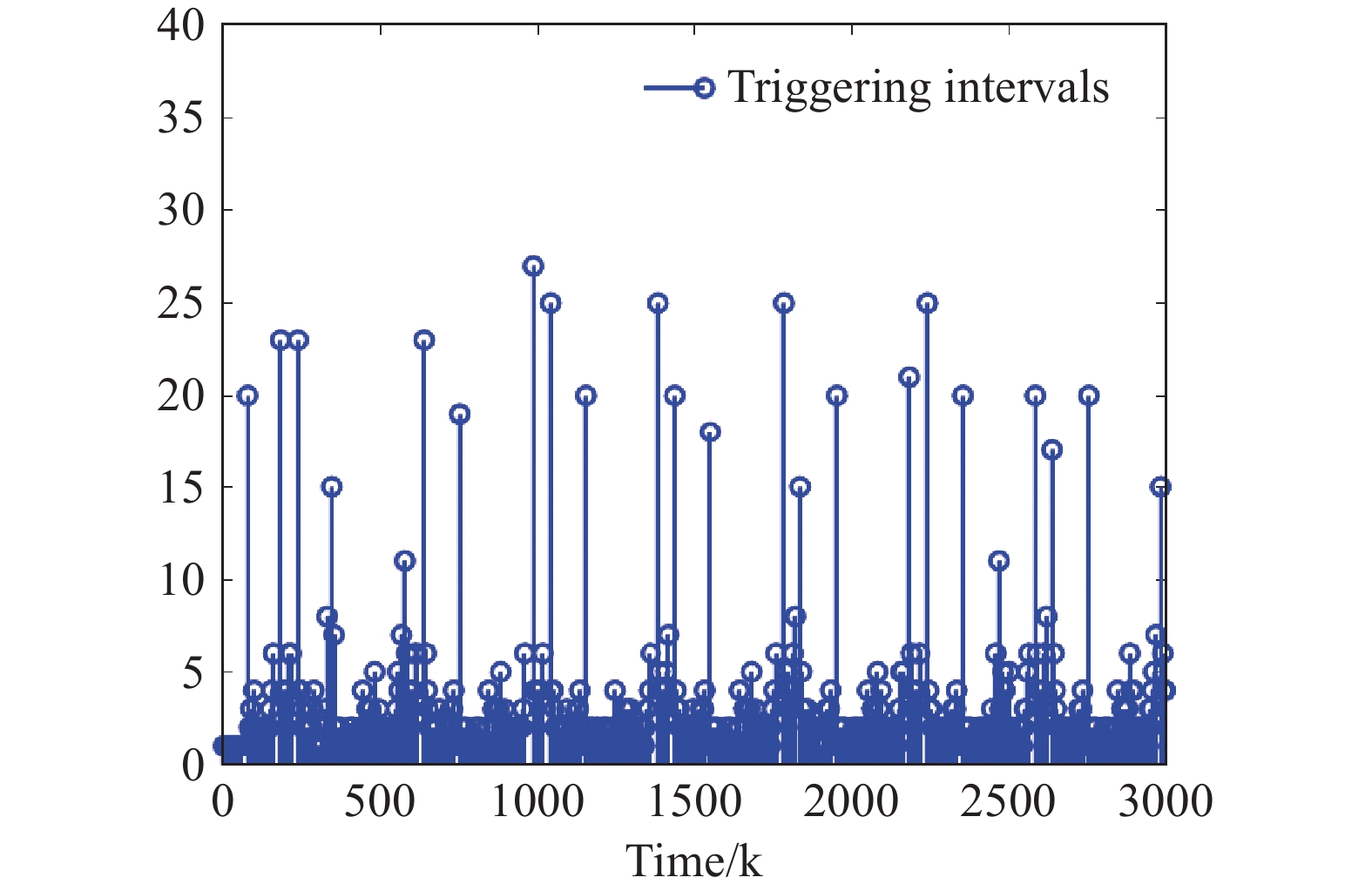
Figure 4. The time intervals between two adjacent triggering instants.

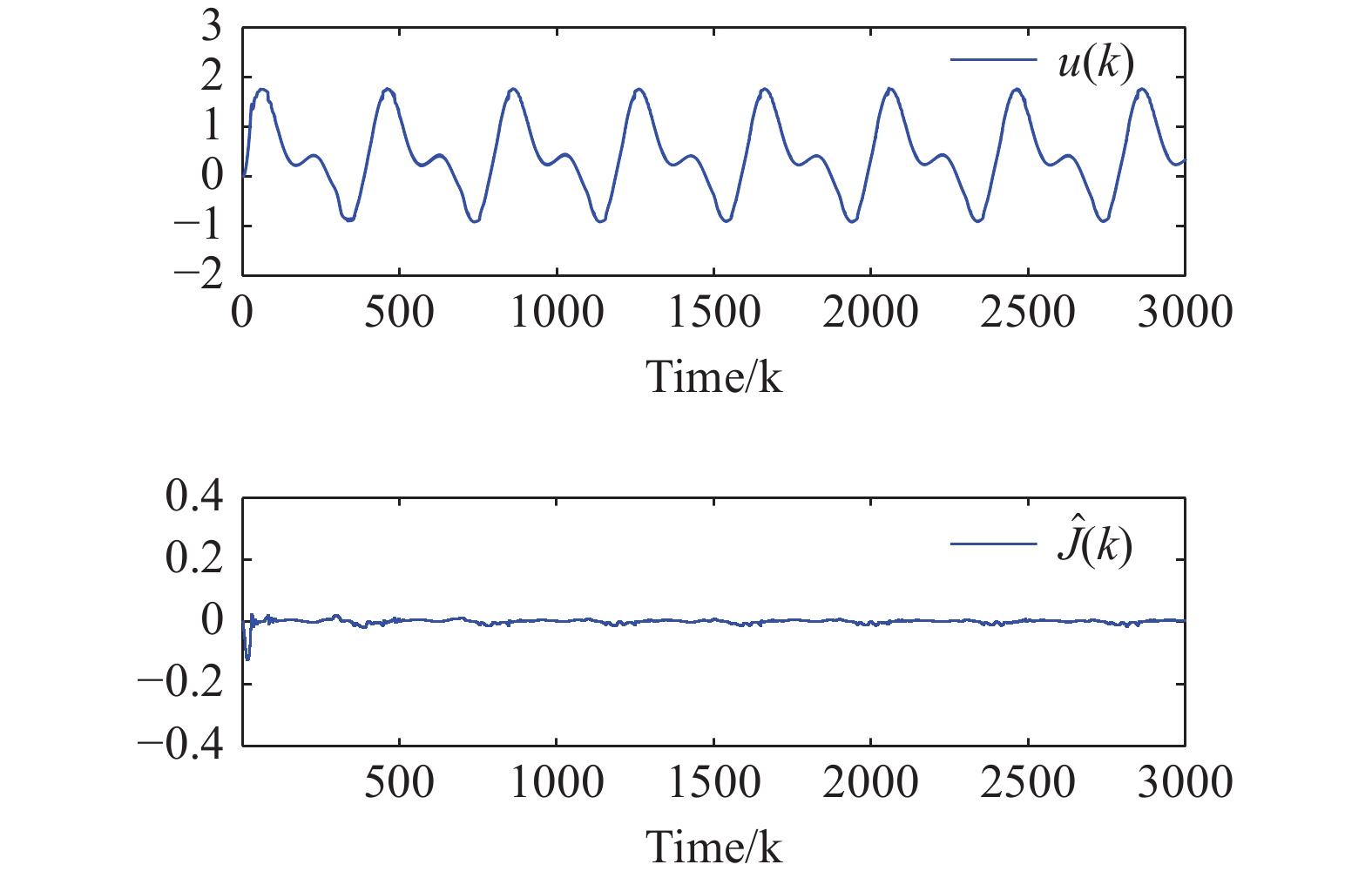
Figure 5. The actual control input \( u(k) \) and the estimated system long-term performance measure \( \hat{J}(k) \).

Figure 6. The 2-norms of the state observer NN weights.

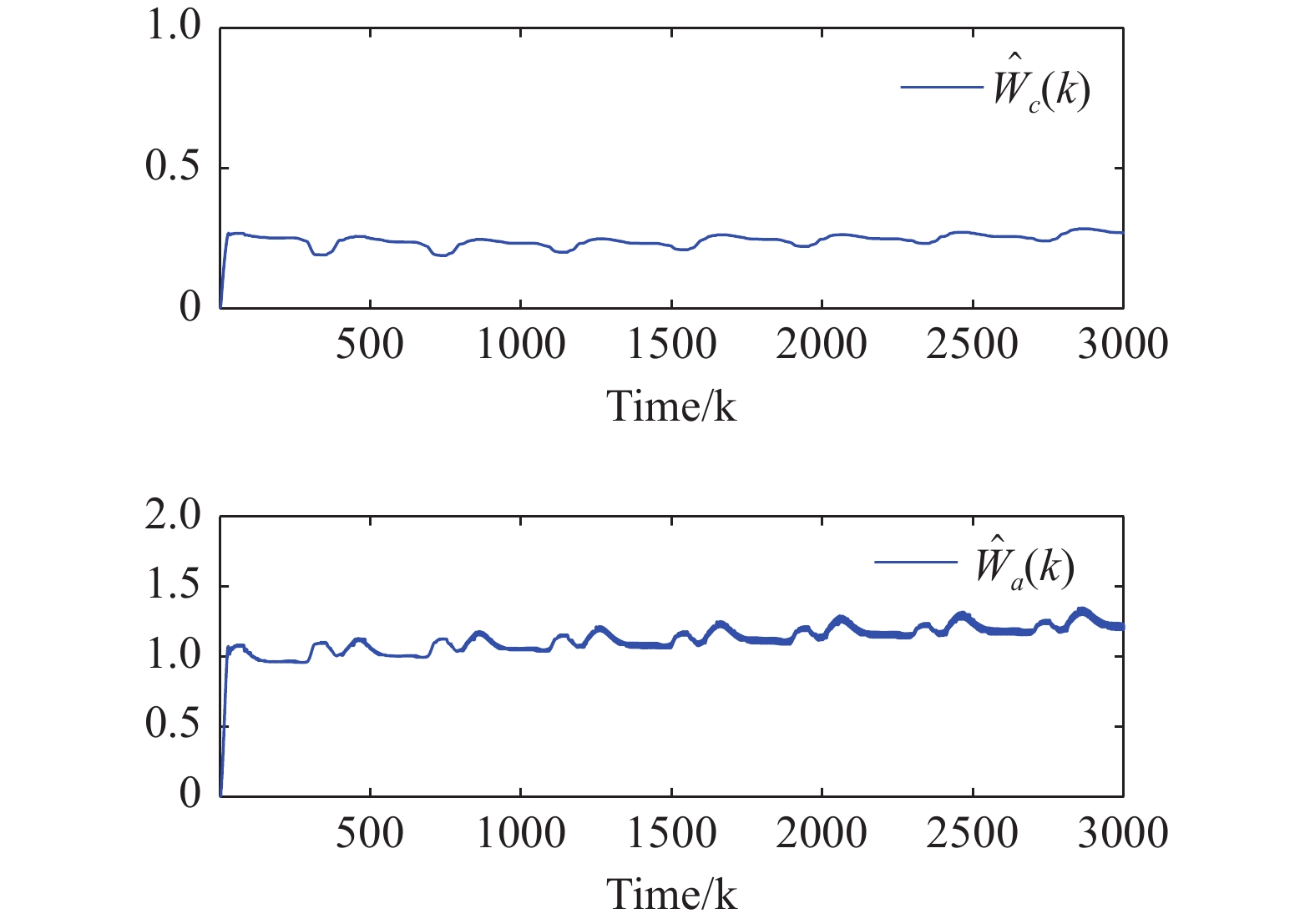
Figure 7. The 2-norms of the critic NN weights and the action NN weights.

Figure 8. The tracking errors presented in this paper and in [44].

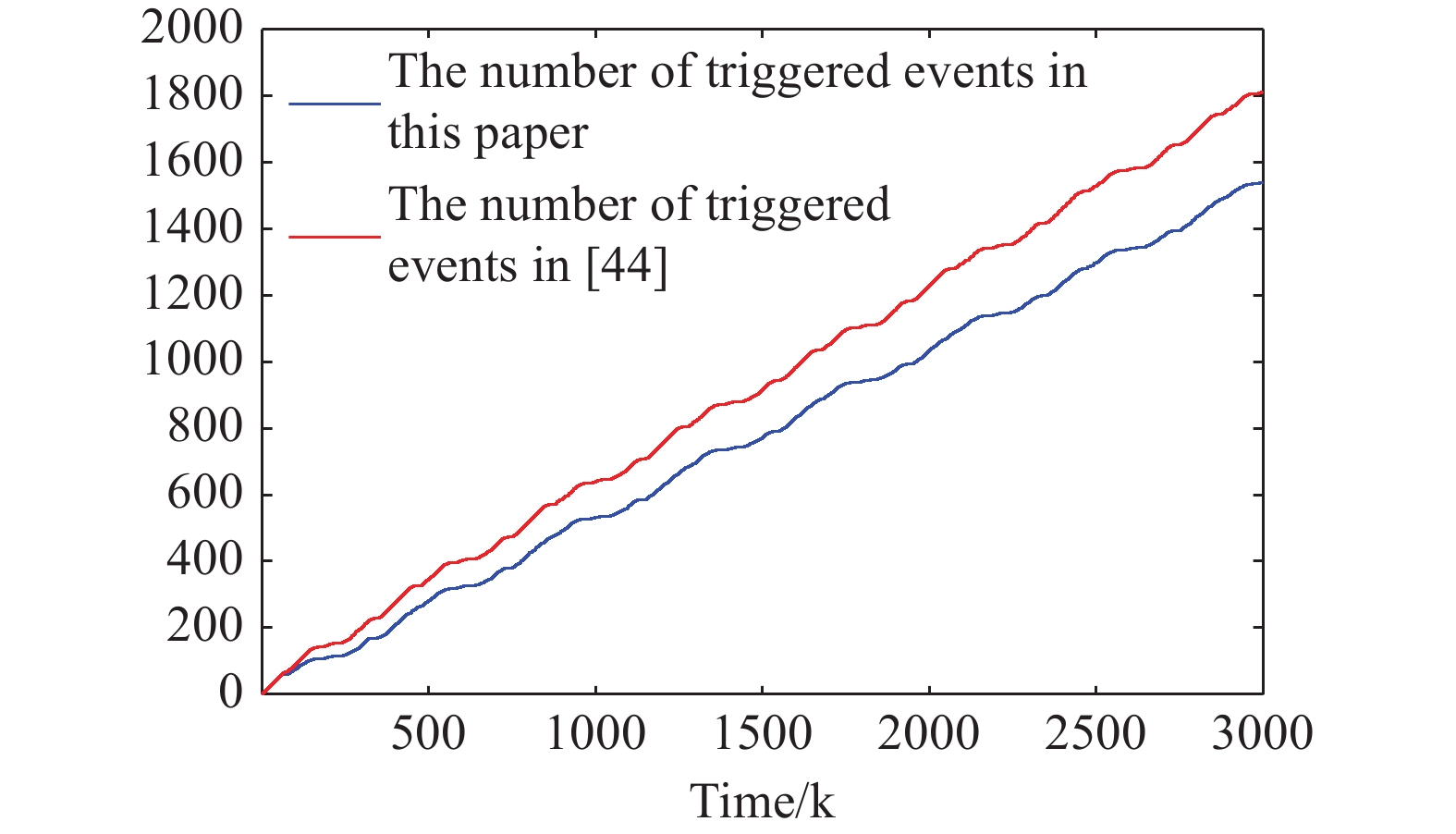
Figure 9. The number of triggered events presented in this paper and in [44].

Furthermore, we compare the developed ET output-feedback optimal tracking control scheme with the traditional ET adaptive neural network tracking control scheme presented in [44]. Figure 8 and Figure 9 display the tracking errors and the number of triggered events presented in this paper and in [44]. According to Table 1, the proposed ET output-feedback optimal tracking control method in this paper obtains smaller mean square tracking errors (MSTE) and fewer triggered events. The simulation results demonstrate the effectiveness of the proposed control scheme.

Table 1 Comparisons of the ET Optimal Tracking Controller and the ET Adaptive NN Tracking Controller

Simulation comparisons	MSTE	Trigger rate
The ET optimal tracking controller	0.0022	51.2%
The ET Adaptive NN tracking controller	0.0028	60.4%

7. Conclusion

In this paper, a novel ET output-feedback optimal tracking control scheme has been developed for a class of uncertain DTPFN systems. The neural state observer has been constructed to estimate the immeasurable system states in real time. In order to overcome the causal contradiction difficulty, the variable substitution approach has been applied to design the tracking controller, which prevents the n-step time delays caused by the traditional n-step-ahead prediction method. Under the ACD framework, the critic NN and the action NN have been constructed to design the optimal tracking controller. The action NN weight updating law has been designed based on the variable substitution approach, which guarantees the optimal tracking control performance. To save communication network resources between the sensor and the controller, a novel ET condition has been developed. According to the Lyapunov stability analysis, all the closed-loop system signals have proven to be UUB. Numerical simulation results have been represented to verify the effectiveness of the proposed method. In the future, it is expected to extend the control scheme proposed in this paper for DTPFN systems with other phenomena, such as state constraints [55] and actuator faults [56]. Additionally, the learning and optimal control of DTPFN systems constitutes another interesting topic [57].