
Downloads
Download


This work is licensed under a Creative Commons Attribution 4.0 International License.
Article
A Novel Multi-Objective Optimization Approach with Flexible Operation Planning Strategy for Truck Scheduling
Yiming Wang , Weibo Liu *, Chuang Wang , Futra Fadzil , Stanislao Lauria , and Xiaohui Liu
Department of Computer Science, Brunel University London, Uxbridge, Middlesex, UB8 3PH, United Kingdom
* Correspondence: Weibo.Liu2@brunel.ac.uk
Received: 11 March 2023
Accepted: 25 April 2023
Published: 23 June 2023
Abstract: The transportation system plays an important role in the open-pit mine. As an effective solution, smart scheduling has been widely investigated to manage transportation operations and increase transportation capabilities. Some existing truck scheduling methods tend to treat the critical parameter (i.e., the moving speed of the truck) as a constant, which is impractical in real-world industrial scenarios. In this paper, a multi-objective optimization (MOO) algorithm is proposed for truck scheduling by considering three objectives, i.e., minimizing the queuing time, maximizing the productivity, and minimizing the financial cost. Specifically, the proposed algorithm is employed to search continuously in the solution space, where the truck moving speed and truck payload are chosen as the operational variables. Moreover, a smart scheduling application integrating the proposed MOO algorithm is developed to assist the user in selecting a suitable scheduling plan. Experimental results demonstrate that our proposed MOO approach is effective in tackling the truck scheduling problem, which could satisfy a wide range of transportation conditions and provide managers with flexible scheduling options.
Keywords:
truck scheduling problem multi-objective optimization open-pit mine1. Introduction
Minerals are important materials in various industries such as the semiconductor, construction, energy, and manufacturing [1-3]. Currently, the mining industry has made contributions to over 4% of the global gross domestic product, thereby becoming one of the most valuable sources of the economic growth for many countries. It is evident that the mining industry is closely related to daily life and will continue to shape the global industry, business, and economy in next decades [4].
Open-pit mining is a highly complex system which takes into account factors such as the environmental conditions, mining operations, and activity organisation [5]. With the growing complexity of mining, it is vital to develop a digital system to monitor the entire mining operation depending on a variety of sensing equipment. In recent years, some artificial-intelligence-based methods have been used to simulate complex mining operations by exploiting data collected from digital mines, and most of these methods have been proposed to solve transport problems [6-10].
Operations of an open-pit mining system involve mineral extraction, transportation, and processing. Among them, the transportation budgets often account for more than half of the total budget of mining operations due to the high cost of fuel and labor [11,12]. Therefore, in order to save budgets, it is crucial to improve the transport efficiency of the open-pit mine. In general, the purpose of the transportation system is to deliver minerals from the open-pit mine to the plant by employing truck fleets. Under such circumstances, rational scheduling of trucks is key to increase productivity and save financial costs. Additionally, some other important objectives also need to be considered such as saving truck queuing time [12] and minimizing ore grade deviation [13].
It is worth noting that the two main objectives (i.e., gaining productivity and saving costs) of the truck scheduling problem are often conflicting. Specifically, productivity would only increase when more trucks are utilized, which inevitably results in additional costs. To address the problem of conflicting objectives, the well-known multi-objective optimization (MOO) algorithms have been introduced into truck scheduling systems [12-15]. Many decision variables (e.g., the truck loading and unloading time, the loading capacity, and the truck moving speed) are treated as constants in existing MOO-based truck scheduling methods, which makes the system impractical in real-world scenarios [13,16,17]. In reality, for safety reasons (such as weather and traffic conditions), these decision parameters (especially the truck moving speed) should not be fixed values. It is challenging to deal with incomplete data for truck scheduling. Specifically, most of existing truck scheduling methods have been applied to large-scale mining systems, which indicates that the collected data is complete and abundant. Nonetheless, small-scale mining systems may suffer from data deficiency due to the lack of sensing devices. Currently, only a few researchers have focused on the small-scale mining operation scheduling problem. To sum up, there is an urgent need to develop a novel MOO-based approach that takes both data quality and system flexibility into account for truck scheduling.
Motivated by the above discussions, a new MOO-based truck scheduling method is proposed in this paper for open-pit mining to optimize the truck moving speed and the truck payload in a flexible way. The proposed MOO algorithm is applied to solve a given truck scheduling problem, and is validated on a small-scale mining database. The main contributions of this paper can be summarized as follows.
 A new truck scheduling problem with higher flexibility is presented. Different from the existing studies that treat many operational parameters as constants, this paper regards the truck speed and payload as decision variables for optimization, which allows for the operational flexibility for truck drivers.
A new truck scheduling problem with higher flexibility is presented. Different from the existing studies that treat many operational parameters as constants, this paper regards the truck speed and payload as decision variables for optimization, which allows for the operational flexibility for truck drivers.
 A new MOO-based trucking scheduling model is established for open-pit mining. This is the first work in this field that fully considers the truck speed, payload and mandatory breaks for the drivers, which could alleviate the risk of imprecise task scheduling caused by human intervention.
A new MOO-based trucking scheduling model is established for open-pit mining. This is the first work in this field that fully considers the truck speed, payload and mandatory breaks for the drivers, which could alleviate the risk of imprecise task scheduling caused by human intervention.
 An application tool is developed which could assist users in designing an appropriate scheduling plan for specific working conditions.
An application tool is developed which could assist users in designing an appropriate scheduling plan for specific working conditions.
 Extensive experiments are conducted on a real-world small-scale transportation dataset to verify the effectiveness of the proposed approach.
Extensive experiments are conducted on a real-world small-scale transportation dataset to verify the effectiveness of the proposed approach.
The remainder of this paper is organized as follows. Section 2 introduces the background of the open-pit mine transportation system and the existing research on truck scheduling problems. Section 3 gives the details of the mathematical model and the optimization method. Experimental results and analysis are described in Section 4. Finally, this paper is concluded in Section 5.
2. Related Work
2.1. Truck Scheduling Problem
In an open-pit mine, the issue of truck scheduling is to strategically organize a fleet of trucks and loaders so as to load and transport minerals efficiently. Traditionally, the scheduling process has been managed by human operators, and its effectiveness is dependent heavily on the prior experience and knowledge. This kind of scheduling strategy is a long process of trial-and-error, and lacks the explicit theoretical support to assist managers in optimizing their decisions. With the development of the digital mining technology, more sensors and monitoring devices have been deployed in the mining systems. A large amount of historical data (sampled by sensors) provides an opportunity to solve data-driven vehicle scheduling problems in mining systems, which makes it possible for the use of mathematical modelling and optimization theories to further improve the scheduling performance. Consequently, researchers have turned to employ the evolutionary optimization methods to solve the complex operational scheduling problem. The evolutionary optimization method is capable of discovering a globally optimal solution in parameter optimization. Early studies have tended to investigate the single-objective optimization approaches, see [10,18-21]. With the growing complexity of mining systems, the simple single-objective optimization algorithms fail to satisfy the performance requirements of the truck scheduling problem because more variables (e.g., weather and traffic conditions) need to be considered. Therefore, the MOO algorithm becomes a proper candidate solution to tackle such a multi-objective truck scheduling problem [13,17].
As a branch of evolutionary computation, the MOO algorithm aims to discover a set of optimal decision variables by minimizing or maximizing the objective functions. Different from the single-objective optimization problem, the MOO problem needs to optimize multiple conflicting objectives simultaneously. The answer to the MOO problem is a set of compromised solutions, referred to as non-dominant solutions, and such an answer defines the optimal trade-off between competing objectives. The non-dominant solutions are also called the Pareto front which is superior to other solutions. Till now, many efforts have been devoted to obtaining the optimal Pareto front by developing advanced evolutionary-based algorithms, such as the strength Pareto evolutionary algorithm II (SPEA2)[22], the non-dominated sorting genetic algorithm II (NSGA-II) [23], and the multi-objective evolutionary algorithm based on the decomposition (MOEA/D) algorithm [24].
Recently, the MOO algorithms, as a useful tool for decision-making and operational planning, have been successfully applied to the open-pit mine truck scheduling problem. A typical example is [17], where an evolutionary MOO algorithm has been employed to schedule the truck allocation and travel trajectories by maximizing the production and minimizing the fuel cost. As for the truck scheduling problem, the commonly-used objective functions are maximizing the production, minimizing the fuel cost, minimizing the queuing time, and minimizing the ore grade deviation [20,21,25]. Some existing studies have mainly focused on dealing with the truck-shovel allocation problem in open-pit mining systems, see [10,13,17]. In such systems, there exist a number of loading and unloading points located at different sites. A fleet of trucks travels on different load-unload trajectories and the MOO algorithm is utilized to find an optimal route.
Although the truck-shovel allocation system has been successfully applied in large-scale mining operations, it is not feasible in small-scale mining systems for the following reasons. First, the truck-shovel allocation system is generally suitable for large-scale mining operations with large mining areas, big data collection and processing systems, various sensing equipment, global positioning system (GPS) data, high-speed network connection, and complex hardware-software configuration. Furthermore, in order to be suitable for large-scale mining operations, the truck-shovel system focuses on complex trajectory planning problems, in which some useful variables need to be treated as constants such as the truck travelling speed and the mandatory breaks for the drivers. In this respect, there is less flexibility in the large-scale mining system as all operations have to be completed on time. On the contrary, small-scale mining systems relax the stringent requirements of route planning due to fewer loading points, which makes mining operations more flexible. For example, when working conditions change, the workers can determine the truck speed and the break time by using different scheduling plans. Based on the above discussions, this paper aims to design a flexible scheduling system for a small-scale mine.
2.2. Transportation Process and Data
The data used in this paper are collected from a small-scale open-pit mine in Norway, which contains the base operating time and the traveling distance of trucks during each payload operation cycle. To provide a clear description of the dataset, the whole transportation process is introduced. The whole transportation operation can be regarded as a repeatable payload cycle, where the payload period of the truck is a cycle of production loading and transport. As shown in Figure 1, a typical payload period is divided into four steps: 1) traveling from the dumping point to the loading point of the open-pit mine; 2) queuing at the loading point and then loading the products; 3) traveling from loading point to the dumping point; and 4) unloading the products at the dumping point. Therefore, the data recorded in a payload period includes: 1) the travel empty time (the time for the truck to travel from the dumping point to the loading point); 2) the stopped empty time (the queuing time of the truck at the loading point); 3) the loading time (the time taken by the truck to load the product at the loading point); 4) the travel loaded time (the time for the truck to travel from the loading point to the dumping point); 5) the unloading time (the time taken by the truck to unload the products); 6) the travel distance (the distance between the loading point and the dumping point); and 7) the payload tonnes (the weight of products being loaded).

Figure 1. Transportation.
There is a wheel loader and two shovels at the loading point. The shovel picks up the material from the pit, transfers it to the loader, and finally loads it on the wheels. Compared to the truck-shovel system that directly uses the shovel to load the truck, the wheel loader has two advantages: 1) the loading time is relatively stable and 2) the weight of materials being loaded is controllable. Note that the information about payload weight is shared by the loader operator when the truck is being loaded. The operators could stop the load at any time to control the weight of the payload. This payload system provides a flexible way to control the payload and it is, therefore, much easier to manage the time and payload in the truck scheduling system.
Apart from the payload period, the worker shift cycle is also a key factor for the truck scheduling issue. There are three worker shift operations in a day: the day-shift (7:00 AM - 3:00 PM), afternoon-shift (3:00 PM - 11:00 PM), and night-shift (11:00 PM - 07:00 AM). During each shift, the workers repeat the payload period and are expected to have a rest time about 45 minutes. It should be noted that all workers take a rest at the same time since the wheel loader also needs to rest and stop during the entire payload period. It is well-known that working conditions at night are different from those at daytime and that the day and afternoon shifts are often scheduled at the same operations, while the night shifts are different. Sometimes, night shifts are not even scheduled. Considering the entire transport process, it is clear that all trucks follow the same trajectory. In this context, it is not necessary to consider the route planning. Therefore, the truck speed and payload weight should be chosen as operational variables.
3. A Multi-Objective Optimization Algorithm for Truck Scheduling Problems
3.1. Decision Variables
In order to obtain optimal transportation efficiency, we select five parameters as decision variables, including the loaded speed, empty speed, payload, fleet size, and worker shift. Moreover, two modes (i.e., day and night) are taken into account in the truck scheduling problem. More details are described in Table 1. Note that the loading time and the unloading time are also important parameters. We find that they are stable in the payload cycle. Thus, in this paper, the loading time and unloading time are set as the constants, denoted by  and
and  , respectively.
, respectively.
Table 1. The decision variables of the truck scheduling problem

3.2. Problem Formulation
1) Minimizing Queuing Time: In a truck scheduling system, the loading queue at the loading point is the main reason that leads to inefficient use of the trucks. Therefore, it is necessary to minimize the queuing time of trucks. First, we should clarify how the loading queue is generated. Generally, when the loading time is longer than the time interval between adjacent trucks, this arrangement will result in a queue, as shown in Figure 2.

Figure 2. Illustration of the emergence of queue.
When a group of trucks travel over a period of time, the time intervals between each pair of neighboring trucks would be similar after a few rounds of adjustment. The queue will occur when the loading time exceeds the time interval. For example, assuming an interval of four minutes and a loading time of five minutes, a truck arrives at the loading point every four minutes. At the loading point, the former is still loading when the latter arrives, so the latter has to wait for one minute before starting to load. Based on this fact, the mathematical modelling method is used to calculate the queuing time. The detailed modelling strategy and the corresponding parameters are given as follows.
Travel empty time (denoted by  ) refers to the time for a truck to travel from the point of unloading to the point of loading.
) refers to the time for a truck to travel from the point of unloading to the point of loading.
Travel loaded time (denoted by  ) means the time that a truck takes to travel from the loading point to the unloading point.
) means the time that a truck takes to travel from the loading point to the unloading point.
Travel time (denoted by  ) is the total time that a truck takes to load products and travel during a work cycle.
) is the total time that a truck takes to load products and travel during a work cycle.
Travel time interval (denoted by  ) denotes the time between two trucks arriving at the loading point one after the other.
) denotes the time between two trucks arriving at the loading point one after the other.
Motivated by the above discussions, the first objective of this paper is to minimize the queuing time, which is expressed as follows:

2) Maximizing Production: The main goal of truck scheduling is to maximize the production. It has been demonstrated that this objective function is adopted in most existing studies of truck scheduling problems [13,16,17]. Different from some existing studies that only focus on maximizing the production during a specific payload period, this paper proposes an alternative approach to compute the total amount of the production in a full day. This makes the problem more complex, since the rest periods of workers and the different productivity (between day and night shifts) need to be taken into account.
During a working day, three workers operate in shifts, with the day and afternoon shifts following the same scheduling strategy while the night shift using a different scheduling strategy. In an 8-hour worker shift, the working time is divided into many repeatable payload cycles. The definition of payload cycle is introduced in Section 2.2. To calculate the total products, the step-by-step modelling method is employed and the corresponding parameters are given as follow.
First, the payload cycle time describes the time that a truck takes to complete the whole payload cycle, which is calculated by  . Considering the different operations performed during the day and night, the payload cycle time is also calculated for day and night shifts which are denoted by
. Considering the different operations performed during the day and night, the payload cycle time is also calculated for day and night shifts which are denoted by  and
and  , respectively.
, respectively.
Then, apart from the case of rest periods, the working time of a worker shift is expressed as  , where
, where  is the resting time. Given the working time and the payload cycle time, it is possible to calculate a so-called count to describe how many payload cycles a truck fleet completes during an 8-hour worker shift. The count is expressed as
is the resting time. Given the working time and the payload cycle time, it is possible to calculate a so-called count to describe how many payload cycles a truck fleet completes during an 8-hour worker shift. The count is expressed as  , where
, where  is the floor function that returns the greatest integer less than the input value. Taking into account the difference between day and night shifts, the counts are denoted by
is the floor function that returns the greatest integer less than the input value. Taking into account the difference between day and night shifts, the counts are denoted by  and
and  for day and night shifts, respectively.
for day and night shifts, respectively.
Finally, the production of each worker shift is calculated by  . The total production for a day is obtained by summing the total production of all three worker shifts.
. The total production for a day is obtained by summing the total production of all three worker shifts.
Therefore, the second objective of this paper is described by

where  is the maximum production. In this setting, both the day shift and the afternoon shift have two identical operations. Different from both the day shift and the afternoon shift, the night shift operation can only be executed when
is the maximum production. In this setting, both the day shift and the afternoon shift have two identical operations. Different from both the day shift and the afternoon shift, the night shift operation can only be executed when  , indicating that the night shift is available.
, indicating that the night shift is available.
3) Minimizing Cost: Over half of the total budget of open-pit mining has been spent on the transportation operation. Thus, saving financial cost is another objective that needs to be considered in the truck scheduling problem. In the transportation operation, the cost consists of two parts: the fuel cost and driver payment. The fuel consumption per kilometer is affected by four factors: the road conditions, truck characteristics, speed, and payload. Among them, the road conditions and truck characteristics are not significant since they are fixed in this transport system. In addition, the effect of speed is practically insignificant, as the trucks move slowly. The fuel costs only increase when trucks move at high speeds (over 64km/h) [26]. Therefore, the only factor that would significantly affect the cost of fuel is the payload.
It has been shown in [27] that the fuel cost of a truck and the payload are linearly correlated. To illuminate this linear relation, a line plot is provided where each asterisk represents a sample featured by the payload and fuel cost per kilometer, as shown in Figure 3. The fuel cost (  ) is predicted for a given payload
) is predicted for a given payload  by fitting the fuel cost and payload data with a linear regression model, denoted by
by fitting the fuel cost and payload data with a linear regression model, denoted by  .
.

Figure 3. Linear relation between payload and fuel cost.
Thus, the cost of fuel in US dollars is expressed as follows:

where  is the fuel cost (
is the fuel cost ( 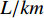 ) of a truck while travelling empty and
) of a truck while travelling empty and  denotes the price of the diesel fuel in US dollars.
denotes the price of the diesel fuel in US dollars.
The second part of the transportation cost is the salaries of workers. It is known that the shift cycle of worker consists of two 8-hour day shifts (day and afternoon) and one 8-hour night shift, and thus the salaries of workers can be estimated by

where  and
and  represent the payment for the worker on day and night shifts, respectively; and
represent the payment for the worker on day and night shifts, respectively; and  and
and  are the fleet sizes of the trucks which are the same as the numbers of the workers.
are the fleet sizes of the trucks which are the same as the numbers of the workers.
The third objective of this paper is formulated as follows:

3.3. MOO Algorithm
It can be seen that the above-mentioned objectives are conflicting. For example, maximizing production will naturally require more equipment and working hours, which obviously conflicts with minimizing the cost. On the other hand, when more trucks operate simultaneously, it increases production but causes more queuing time. In this context, there are no optimal solutions that achieve all three objectives at the same time. The MOO algorithm, therefore, becomes an appropriate way to solve this problem.
Instead of directly looking for the optimal solutions, the MOO algorithm attempts to find optimal trade-off solutions among all the objectives that are known as the non-dominated solutions or the Pareto optimal solutions. As many non-dominated solutions can potentially be similar to each other, it is necessary to keep the diversity and reduce the similarity of all the solutions by selecting some representative solutions, known as the Pareto front. In other words, the MOO algorithm aims to find a set of diverse and optimal solutions that provide trade-offs among all objectives.
Most existing MOO methods are based on the evolutionary algorithm due to its fast convergence and high effectiveness characteristics. These MOO algorithms simulate the process of the natural selection, where better individuals (from the population of the parent generation) are selected, recombined and added to the subsequent generation of children. After several iterations, the optimal individuals (solutions) are selected to form a Pareto front. Most evolutionary-based MOO algorithms aim to develop a selection strategy that selects individuals with higher fitness and maintains the diversity of the populations.
In this paper, four popular MOO algorithms are employed to solve the formulated truck scheduling problem.
NSGA-II: The non-dominated sorting genetic algorithm II (NSGA-II) [23] introduces the crowding distance calculation within a cuboid region to rank the members of the population, which can maintain good spread of solutions. The NSGA-II is a fast and effective algorithm for solving MOO problems.
SPEA2: The strength Pareto evolutionary algorithm II (SPEA2) [22] incorporates a nearest neighbor density metric into the calculation of fitness function. Intuitively, the individuals with more neighbors have less chances to be selected. This strategy guarantees a broader distribution of the selected individuals.
PESA-II: The Pareto envelope-based selection algorithm II (PESA-II) [28] combines the evolutionary algorithm with the region-based selection strategy instead of the individual-based selection strategy. The PESA-II considers the grid crowding degree during selection. This strategy effectively reduces the probability of selecting the similar individuals (within the same grid) and ensures good spread along the Pareto front.
MOEA/D: The multi-objective evolutionary algorithm based on decomposition (MOEA/D) [24] decomposes an MOO problem into a set of sub-problems and uses the evolutionary algorithm to optimize the sub-problems simultaneously. The MOEA/D has not addressed the diversity of the selected solutions specifically.
To handle the truck scheduling problem, the MOO models are established and a group of Pareto fronts are produced, thereby providing the users the opportunity to choose desirable solutions among the obtained results.
3.4. User Application
Although the MOO model gives users the flexibility to select appropriate operations, there is still one issue that needs to be addressed. That is, once an MOO model is obtained, the solutions will be fixed. In this context, a fixed MOO model may eventually become inaccurate because worker salaries and fuel costs change over time. Moreover, the distance between the loading and unloading points may be different, as the loading point is not always fixed. Therefore, it is necessary to design a user application that allows the user to update the MOO model by customizing the worker payment, fuel cost, and travel distance.
A user application is shown in Figure 4 where in the left panel, the users can manually input the distance, the loading time, the unloading time, the worker payment, and the fuel cost according to the instant situations. By clicking the “Load model” button, an MOO model learned with default settings will be loaded and the Pareto fronts will be shown in the table area. Alternatively, the users can choose an MOO algorithm from the four candidates and click the “Run MOO” button, such that a new MOO model can be obtained and its solutions are also displayed in the table area.

Figure 4. User application with graphic interface.
It is worth noting that many candidate solutions are suggested in the table area. In order to assist the user in decision making, the user application is designed with features that the user can narrow down the possible choices in several parameters provided by the user application. For example, when the users select the “low speed” option, all the solutions with a “high speed” (the truck speed is higher than the average speed) will be discarded. Then, by clicking the “Show Chart” button, the filtered results will be displayed at the bottom center panel as a bar chart. The first chart (top) illustrates the ten solutions with the maximum productions (sorted from high to low), and the second one (bottom) offers the ten minimum-cost solutions (sorted from low to high). These two charts visualize the solutions to help users determine which solution can be selected.
The final step is to select the desirable solution and assist users to schedule the optimal operation plan which is the timetable of the job chain. To do this, the users need to input the number of the selected solution (from the table or chart) in the “Selected Solution No.” area and click the “Show Timetable” button. Then, a sequence of underlying optimal operations will be displayed in the “Time Stamps” area based on the selected solution. Considering that each truck driver may have different break time preferences, the user application is also designed in a way that users can customize their desired resting clock time by clicking the “Update Timetable” button. Then, the application will update the timestamp and display the sequence timetable with the recent rest time. Note that the operational plan after the resting period is rescheduled accordingly, which ensures that the rescheduled plan does not impact the total production, cost, and queuing time. Meanwhile, the drivers could benefit from the application on the flexibility of scheduling their resting time.
In summary, the advantages of the user application are concluded in the following four aspects: 1) offering a straightforward way to update the MOO model; 2) supporting visual illuminations of the candidate solutions; 3) selecting a solution that satisfies the user requirement; and 4) providing drivers with flexible resting time.
4. Experiment
4.1. Results
A real-world small-scale mine dataset from Norway is prepared for validation in this paper. Detailed information about the dataset is presented in Section 2.2. The dataset consists of 245090 payload cycles collected from four trucks. However, the early data is recorded by the conventional equipment, resulting in the fact that much essential information is missing. Therefore, after data cleaning, only 2136 payload cycles with relatively complete information are extracted. Obviously, this dataset is characterized by the fact that most of the data is incomplete. It is worth pointing out that despite this deficiency, some useful information can still be extracted such as the speed range of the truck, the average truck loading/unloading time, and the payload range. This information allows us to simulate transport operations via mathematical modelling and obtain optimal solutions using the MOO model. The hyper-parameters of the four MOO algorithms include the number of decision variables, the number of objectives, the population size, and the number of generations, which are set to be 9, 3,100 and 100, respectively.
Experimental results of the optimal truck scheduling strategy are shown in Table 2 and the corresponding objective values are shown in Table 3. Normally, the MOO model will produce 100 optimal solutions with different driving speeds in order to give the user more flexibility to choose the suitable operation. Then, the user can select a satisfactory operation from these candidates with the help of the user application.
Table 2. The selected optimal solutions for the truck scheduling problem
| No. | loaded speed (km/h) | empty speed (km/h) | fleet size | payload (ton) | worker shift | |||||||
| day | night | day | night | day | night | day | night | |||||
| 1 | 8.54 | - | 35.03 | - | 3 | - | 209.01 | - | day | |||
| 2 | 26.39 | 25.73 | 40.69 | 35.30 | 5 | 5 | 211.38 | 211.40 | day+night | |||
| 3 | 26.02 | 25.73 | 39.96 | 34.54 | 4 | 4 | 211.40 | 211.39 | day+night | |||
| 4 | 8.52 | - | 7.77 | - | 3 | - | 189.32 | - | day | |||
| 5 | 24.61 | 23.84 | 37.03 | 28.98 | 3 | 4 | 211.40 | 211.38 | day+night | |||
Table 3. The objective values of the selected optimal solutions
| No. | Average queuing time | Production (ton) | Cost ($) |
| 1 | 0 | 18811.30 | 1794.41 |
| 2 | 00:01:02 | 84555.78 | 5980.06 |
| 3 | 00:00:18 | 70183.57 | 4878.82 |
| 4 | 0 | 11899.05 | 15498.93 |
| 5 | 0 | 55385.10 | 3963.91 |
The flexible resting time strategy is illustrated in Figure 5. Specifically, Figure 5(a) and Figure 5(b) present the work plan following the suggested maximum and minimum time, respectively. First, it can be observed that the operations of the two work plans are the same before the break. Then, the operations become different when the resting time is finished. Moreover, when the break time is maximum (which is 1 hour 3 minutes and 59 seconds), the driver can have a longer breaking time and finally, complete all the work plan at exactly the end of the worker shift which is 15:00:00. For the minimum resting time, the driver can take a shorter break time, but finally finish all the work plan and knock off in advance. This application provides more options for drivers to schedule their resting time.

Figure 5. Illustration of the resting starting at different clock time.
5. Conclusion
In this paper, a novel MOO-based truck scheduling method has been developed to provide a practical platform for transportation operations in the open-pit mine. In order to guarantee the system flexibility, this paper has treated the truck speed and payload as operational variables in the scheduling problem. Furthermore, the mandatory rest time has been taken into account, which aims to allow drivers to request a break at any time without affecting the total productivity. Technically, three objectives (which include the queuing time, productivity, and financial cost) have been optimized simultaneously by using the MOO algorithm. Experiments based on the real-world dataset have validated the effectiveness of the proposed method. Future research topics would include 1) designing new MOO algorithms by integrating additional information (e.g., truck electrical information) to improve the flexibility of the application; and 2) applying the proposed method to other transportation systems in the large-scale open-pit mine.
Author Contributions: Yiming Wang: conceptualization, formal analysis, investigation, methodology, soft-ware, visualization, writing —original draft; Weibo Liu: formal analysis, methodology, supervision,writing—original draft, writing—review & editing; Chuang Wang: data curation, formal analysis, investiga-tion, methodology, validation, writing —original draft; Futra Fadzil: project administration, visualization,writing—original draft; Stanislao Lauria: conceptualization, investigation, project administration, resources,supervision, writing—review & editing; Xiaohui Liu: conceptualization, methodology, resources, supervision,writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding: This work was supported by the European Union’s Horizon 2020 Research and Innovation Programme under Grant 869529 (Dig_IT).
Data Availability Statement: Not applicable.
Conflicts of Interest: The authors declare no conflict of interest.
Acknowledgments: We would like thank Titania AS for providing the industrial data.
References
- Hodge, R.A.; Ericsson, M.; Löf, O.; et al. The global mining industry: Corporate profile, complexity, and change. Miner. Econ., 2022, 35: 587−606.
- Addison, T.; Roe, A. Extractives for development. Extr. Ind., 2018, 3.
- Carvalho, F.P. Mining industry and sustainable development: Time for change. Food Energy Secur., 2017, 6: 61−77.
- Humphreys, D. The mining industry after the boom. Miner. Econ., 2019, 32: 145−151.
- Domingues, M.S.Q.; Baptista, A.L.F.; Diogo, M.T. Engineering complex systems applied to risk management in the mining industry. Int. J. Min. Sci. Technol., 2017, 27: 611−616.
- Wang, J.M.; Bi, L.; Wang, L.G.; et al. A mining technology collaboration platform theory and its product development and application to support China’s digital mine construction. Appl. Sci., 2019, 9: 5373.
- Wu, Q.; Xu, H. Three-dimensional geological modeling and its application in digital mine. Sci. China Earth Sci., 2014, 57: 491−502.
- Temkin, I.; Myaskov, A.; Deryabin, S.; et al. Design of a digital 3D model of transport-technological environment of open-pit mines based on the common use of telemetric and geospatial information. Sensors, 2021, 21: 6277.
- Cudjoe, M.N.M.; Cawood, F.T. The tracking of metal content on a surface mine: A digital mining technology approach. Res. Policy, 2022, 76: 102571.
- Zhang, L.J.; Xia, X.H. An integer programming approach for truck-shovel dispatching problem in open-pit mines. Energy Procedia, 2015, 75: 1779−1784.
- Chaowasakoo, P.; Seppälä, H.; Koivo, H.; et al. Improving fleet management in mines: The benefit of heterogeneous match factor. Eur. J. Oper. Res., 2017, 261: 1052−1065.
- Zhang, Y.H.; Zhao, Z.Y.; Bi, L.; et al. Determination of truck-shovel configuration of open-pit mine: A simulation method based on mathematical model. Sustainability, 2022, 14: 12338.
- Zhang, S.; Lu, C.W.; Jiang, S.; et al. An unmanned intelligent transportation scheduling system for open-pit mine vehicles based on 5G and big data. IEEE Access, 2020, 8: 135524−135539.
- Eskandari, H.; Darabi, H.; Hosseinzadeh, S.A. Simulation and optimization of haulage system of an open-pit mine. In Proceedings of 2013 Summer Computer Simulation Conference, Toronto, Ontario, Canada, 7–10 July 2013; Society for Modeling & Simulation International: Toronto, Ontario, Canada, 2013; p. 37.
- Manríquez, F.; González, H.; Morales, N. Short-term open-pit production scheduling optimizing multiple objectives accounting for shovel allocation in stockpiles. Optim. Eng., 2023, 24: 681−707.
- Subtil, R.F.; Silva, D.M.; Alves, J.C. A practical approach to truck dispatch for open pit mines. In Proceedings of 35th APCOM Symposium 2011, Wollongong, Australia; 2011; pp. 765–777.
- Alexandre, R.F.; Campelo, F.; Vasconcelos, J.A. Multi-objective evolutionary algorithms for the truck dispatch problem in open-pit mining operations. Learn. Nonlinear Models, 2019, 17: 53−66.
- Fioroni, M.M.; Franzese, L.A.G.; Bianchi, T.J.; et al. Concurrent simulation and optimization models for mining planning. In Proceedings of 2008 Winter Simulation Conference, Miami, FL, USA, 07–10 December 2008; IEEE: Miami, FL, USA, 2008; pp. 759–767. doi: 10.1109/WSC.2008.4736138.
- Alarie, S.; Gamache, M. Overview of solution strategies used in truck dispatching systems for open pit mines. Int. J. Surf. Min. Reclam. Environ., 2002, 16: 59−76.
- Patterson, S.R.; Kozan, E.; Hyland, P. Energy efficient scheduling of open-pit coal mine trucks. Eur. J. Oper. Res., 2017, 262: 759−770.
- Bastos, G.S.; Souza, L.E.; Ramos, F.T.; et al. A single-dependent agent approach for stochastic time-dependent truck dispatching in open-pit mining. In Proceedings of the 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 05–07 October 2011; IEEE: Washington, DC, USA, 2011; pp. 1057–1062. doi: 10.1109/ITSC.2011.6082902.
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm. ETH Library: Zürich, 2001.
- Deb, K.; Pratap, A.; Agarwal, S.; et al. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput., 2002, 6: 182−197.
- Zhang, Q.F.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput., 2007, 11: 712−731.
- Mohtasham, M.; Mirzaei-Nasirabad, H.; Askari-Nasab, H.; et al. A multi-objective model for fleet allocation schedule in open-pit mines considering the impact of prioritising objectives on transportation system performance. Int. J. Min. Reclam. Environ., 2021, 35: 709−727.
- Greene, D.L. Estimated speed/fuel consumption relationships for a large sample of cars. Energy, 1981, 6: 441−446.
- Ghaffariyan, M.R.; Barrier, C.; Brown, M.; et al. A Short Review of Timber Truck Fuel Consumption Studies. University of the Sunshine Coast: Brisbane, 2018.
- Corne, D.W.; Jerram, N.R.; Knowles, J.D.; et al. PESA-II: Region-based selection in evolutionary multiobjective optimization. In Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco, CA, USA, 7–10 July, 2001; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2007; pp. 283–290.





